Determinant
of a square matrix 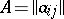 of order
of order  over a commutative associative ring
over a commutative associative ring 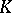 with unit 1
with unit 1
The element of 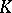 equal to the sum of all terms of the form
equal to the sum of all terms of the form
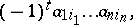 |
where 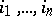 is a permutation of the numbers
is a permutation of the numbers 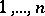 and
and 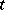 is the number of inversions of the permutation
is the number of inversions of the permutation 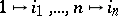 . The determinant of the matrix
. The determinant of the matrix
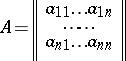 |
is written as
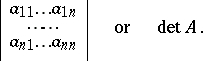 |
The determinant of the matrix 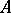 contains
contains 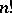 terms; when
terms; when 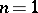 ,
, 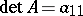 , when
, when 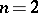 ,
, 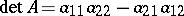 . The most important instances in practice are those in which
. The most important instances in practice are those in which 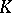 is a field (especially a number field), a ring of functions (especially a ring of polynomials) or a ring of integers.
is a field (especially a number field), a ring of functions (especially a ring of polynomials) or a ring of integers.
From now on, 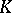 is a commutative associative ring with 1,
is a commutative associative ring with 1, 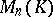 is the set of all square matrices of order
is the set of all square matrices of order  over
over 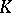 and
and 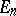 is the identity matrix over
is the identity matrix over 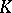 . Let
. Let 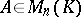 , while
, while  are the rows of the matrix
are the rows of the matrix 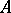 . (All that is said from here on is equally true for the columns of
. (All that is said from here on is equally true for the columns of 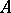 .) The determinant of
.) The determinant of 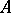 can be considered as a function of its rows:
can be considered as a function of its rows:
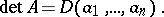 |
The mapping
 |
is subject to the following three conditions:
1) 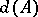 is a linear function of any row of
is a linear function of any row of 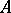 :
:
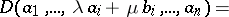 |
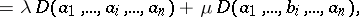 |
where 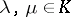 ;
;
2) if the matrix 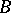 is obtained from
is obtained from 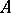 by replacing a row
by replacing a row 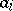 by a row
by a row 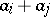 ,
, 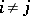 , then
, then 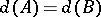 ;
;
3) 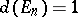 .
.
Conditions 1)–3) uniquely define 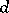 , i.e. if a mapping
, i.e. if a mapping 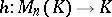 satisfies conditions 1)–3), then
satisfies conditions 1)–3), then 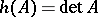 . An axiomatic construction of the theory of determinants is obtained in this way.
. An axiomatic construction of the theory of determinants is obtained in this way.
Let a mapping 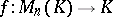 satisfy the condition:
satisfy the condition:
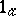 ) if
) if 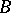 is obtained from
is obtained from 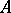 by multiplying one row by
by multiplying one row by 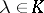 , then
, then 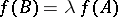 . Clearly 1) implies
. Clearly 1) implies 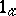 ). If
). If 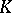 is a field, the conditions 1)–3) prove to be equivalent to the conditions
is a field, the conditions 1)–3) prove to be equivalent to the conditions 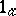 ), 2), 3).
), 2), 3).
The determinant of a diagonal matrix is equal to the product of its diagonal entries. The surjectivity of the mapping 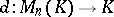 follows from this. The determinant of a triangular matrix is also equal to the product of its diagonal entries. For a matrix
follows from this. The determinant of a triangular matrix is also equal to the product of its diagonal entries. For a matrix
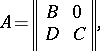 |
where 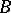 and
and 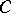 are square matrices,
are square matrices,
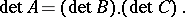 |
It follows from the properties of transposition that 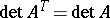 , where
, where 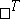 denotes transposition. If the matrix
denotes transposition. If the matrix 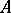 has two identical rows, its determinant equals zero; if two rows of a matrix
has two identical rows, its determinant equals zero; if two rows of a matrix 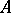 change places, then its determinant changes its sign;
change places, then its determinant changes its sign;
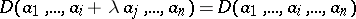 |
when 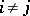 ,
, 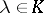 ; for
; for 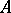 and
and 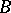 from
from 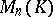 ,
,
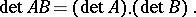 |
Thus, 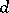 is an epimorphism of the multiplicative semi-groups
is an epimorphism of the multiplicative semi-groups 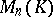 and
and 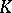 .
.
Let 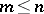 , let
, let 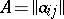 be an
be an 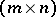 -matrix, let
-matrix, let 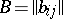 be an
be an 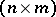 -matrix over
-matrix over 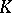 , and let
, and let 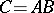 . Then the Binet–Cauchy formula holds:
. Then the Binet–Cauchy formula holds:
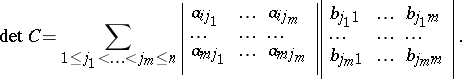 |
Let 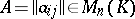 , and let
, and let 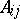 be the cofactor of the entry
be the cofactor of the entry 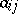 . The following formulas are then true:
. The following formulas are then true:
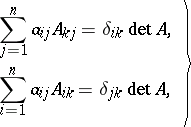 | (1) |
where 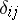 is the Kronecker symbol. Determinants are often calculated by development according to the elements of a row or column, i.e. by the formulas (1), by the Laplace theorem (see Cofactor) and by transformations of
is the Kronecker symbol. Determinants are often calculated by development according to the elements of a row or column, i.e. by the formulas (1), by the Laplace theorem (see Cofactor) and by transformations of 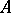 which do not alter the determinant. For a matrix
which do not alter the determinant. For a matrix 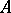 from
from 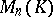 , the inverse matrix
, the inverse matrix 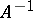 in
in 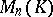 exists if and only if there is an element in
exists if and only if there is an element in 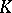 which is the inverse of
which is the inverse of 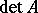 . Consequently, the mapping
. Consequently, the mapping
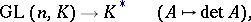 |
where 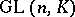 is the group of all invertible matrices in
is the group of all invertible matrices in 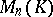 (i.e. the general linear group) and where
(i.e. the general linear group) and where 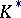 is the group of invertible elements in
is the group of invertible elements in 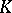 , is an epimorphism of these groups.
, is an epimorphism of these groups.
A square matrix over a field is invertible if and only if its determinant is not zero. The  -dimensional vectors
-dimensional vectors  over a field
over a field 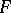 are linearly dependent if and only if
are linearly dependent if and only if
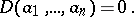 |
The determinant of a matrix 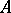 of order
of order 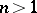 over a field is equal to 1 if and only if
over a field is equal to 1 if and only if 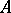 is the product of elementary matrices of the form
is the product of elementary matrices of the form
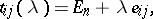 |
where 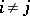 , while
, while 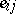 is a matrix with its only non-zero entries equal to 1 and positioned at
is a matrix with its only non-zero entries equal to 1 and positioned at 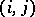 .
.
The theory of determinants was developed in relation to the problem of solving systems of linear equations:
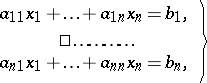 | (2) |
where 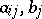 are elements of the field
are elements of the field 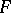 . If
. If 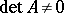 , where
, where 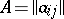 is the matrix of the system (2), then this system has a unique solution, which can be calculated by Cramer's formulas (see Cramer rule). When the system (2) is given over a ring
is the matrix of the system (2), then this system has a unique solution, which can be calculated by Cramer's formulas (see Cramer rule). When the system (2) is given over a ring 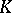 and
and 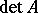 is invertible in
is invertible in 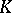 , the system also has a unique solution, also given by Cramer's formulas.
, the system also has a unique solution, also given by Cramer's formulas.
A theory of determinants has also been constructed for matrices over non-commutative associative skew-fields. The determinant of a matrix over a skew-field 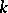 (the Dieudonné determinant) is introduced in the following way. The skew-field
(the Dieudonné determinant) is introduced in the following way. The skew-field 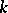 is considered as a semi-group, and its commutative homomorphic image
is considered as a semi-group, and its commutative homomorphic image 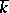 is formed.
is formed. 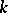 is a group,
is a group, 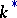 , with added zero 0, while the role of
, with added zero 0, while the role of 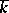 is taken by the group
is taken by the group  with added zero
with added zero 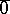 , where
, where  is the quotient group of
is the quotient group of 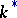 by the commutator subgroup. The epimorphism
by the commutator subgroup. The epimorphism 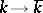 ,
, 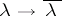 , is given by the canonical epimorphism of groups
, is given by the canonical epimorphism of groups 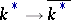 and by the condition
and by the condition 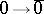 . Clearly,
. Clearly, 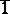 is the unit of the semi-group
is the unit of the semi-group 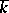 .
.
The theory of determinants over a skew-field is based on the following theorem: There exists a unique mapping
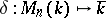 |
satisfying the following three axioms:
I) if the matrix 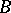 is obtained from the matrix
is obtained from the matrix 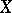 by multiplying one row from the left by
by multiplying one row from the left by 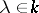 , then
, then 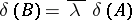 ;
;
II) if 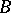 is obtained from
is obtained from 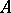 by replacing a row
by replacing a row 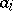 by a row
by a row 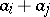 , where
, where 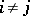 , then
, then 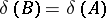 ;
;
III) 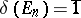 .
.
The element 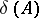 is called the determinant of
is called the determinant of 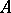 and is written as
and is written as 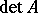 . For a commutative skew-field, axioms I), II) and III) coincide with conditions
. For a commutative skew-field, axioms I), II) and III) coincide with conditions 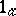 ), 2) and 3), respectively, and, consequently, in this instance ordinary determinants over a field are obtained. If
), 2) and 3), respectively, and, consequently, in this instance ordinary determinants over a field are obtained. If 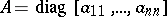 , then
, then 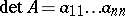 ; thus, the mapping
; thus, the mapping 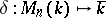 is surjective. A matrix
is surjective. A matrix 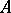 from
from 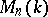 is invertible if and only if
is invertible if and only if 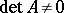 . The equation
. The equation 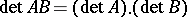 holds. As in the commutative case,
holds. As in the commutative case, 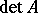 will not change if a row
will not change if a row 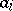 of
of 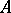 is replaced by a row
is replaced by a row 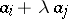 , where
, where 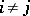 ,
, 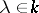 . If
. If 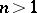 ,
, 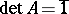 if and only if
if and only if 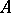 is the product of elementary matrices of the form
is the product of elementary matrices of the form 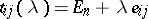 ,
, 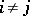 ,
, 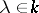 . If
. If 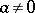 , then
, then
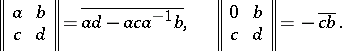 |
Unlike the commutative case, 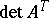 does not have to coincide with
does not have to coincide with 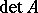 . For example, for the matrix
. For example, for the matrix
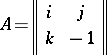 |
over the skew-field of quaternions (cf. Quaternion), 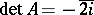 , while
, while 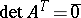 .
.
Infinite determinants, i.e. determinants of infinite matrices, are defined as the limit towards which the determinant of a finite submatrix converges when its order is growing infinitely. If this limit exists, the determinant is called convergent; in the opposite case it is called divergent.
The concept of a determinant goes back to G. Leibniz (1678). H. Cramer was the first to publish on the subject (1750). The theory of determinants is based on the work of A. Vandermonde, P. Laplace, A.L. Cauchy and C.G.J. Jacobi. The term "determinant" was first coined by C.F. Gauss (1801). The modern meaning was introduced by A. Cayley (1841).
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
| [2] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [3] | N.V. Efimov, E.R. Rozendorn, "Linear algebra and multi-dimensional geometry" , Moscow (1970) (In Russian) |
| [4] | R.I. Tyshkevich, A.S. Fedenko, "Linear algebra and analytic geometry" , Minsk (1976) (In Russian) |
| [5] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [6] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [7] | V.F. Kagan, "Foundations of the theory of determinants" , Odessa (1922) (In Russian) |
Comments
References
| [a1] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [a2] | K. Hoffman, R. Kunze, "Linear algebra" , Prentice-Hall (1961) |
| [a3] | M. Koecher, "Lineare Algebra und analytische Geometrie" , Springer (1983) |
| [a4] | S. Lang, "Linear algebra" , Addison-Wesley (1970) |
Determinant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Determinant&oldid=21435