Congruence subgroup
From Encyclopedia of Mathematics
A subgroup  of the general linear group
of the general linear group  over a ring
over a ring  with the following property: There exists a non-zero two-sided ideal
with the following property: There exists a non-zero two-sided ideal  of
of  such that
such that  , where
, where
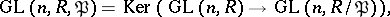 |
that is,  contains all matrices in
contains all matrices in  that are congruent to the unit matrix modulo
that are congruent to the unit matrix modulo 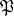 . More generally, a subgroup
. More generally, a subgroup  of a linear group
of a linear group  of degree
of degree  over
over 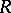 is said to be a congruence subgroup if
is said to be a congruence subgroup if
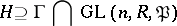 |
for some non-zero two-sided ideal 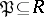 .
.
When
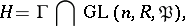 |
 is said to be the principal congruence subgroup corresponding to
is said to be the principal congruence subgroup corresponding to 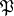 . The concept of a congruence subgroup arose first for
. The concept of a congruence subgroup arose first for 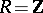 . It is particularly effective and important from the point of view of applications for a Dedekind ring
. It is particularly effective and important from the point of view of applications for a Dedekind ring 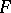 in the case
in the case 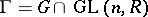 , where
, where 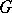 is an algebraic group defined over the field of fractions of
is an algebraic group defined over the field of fractions of 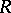 .
.
References
| [1] | H. Bass, J. Milnor, J.-P. Serre, "Solutions of the congruence subgroup problem for 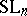 ( ( ) and ) and 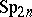 ( (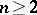 )" Publ. Math. IHES , 33 (1967) pp. 421–499 )" Publ. Math. IHES , 33 (1967) pp. 421–499 |
How to Cite This Entry:
Congruence subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_subgroup&oldid=21411
Congruence subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_subgroup&oldid=21411
This article was adapted from an original article by V.P. Platonov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article