Congruence subgroup problem
Is every subgroup of finite index in 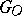 , where
, where 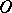 is the ring of integers in an algebraic number field
is the ring of integers in an algebraic number field  (cf. Algebraic number theory) and
(cf. Algebraic number theory) and  is a connected linear algebraic group defined over
is a connected linear algebraic group defined over 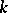 , a congruence subgroup? This is the classical statement of the congruence problem. A contemporary version of it is based on the concept of the congruence kernel, which is a measure of the deviation from a positive solution. Let
, a congruence subgroup? This is the classical statement of the congruence problem. A contemporary version of it is based on the concept of the congruence kernel, which is a measure of the deviation from a positive solution. Let 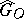 and
and  be the completions of the groups of
be the completions of the groups of 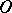 -points of
-points of 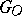 in the topologies defined by all subgroups of finite index and all congruence subgroups of
in the topologies defined by all subgroups of finite index and all congruence subgroups of  , respectively. Then there is a surjective continuous homomorphism
, respectively. Then there is a surjective continuous homomorphism 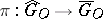 . The kernel of
. The kernel of 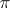 is called the congruence kernel and is denoted by
is called the congruence kernel and is denoted by 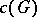 . The positive solution of the classical congruence problem is equivalent to proving
. The positive solution of the classical congruence problem is equivalent to proving  . In its modern form, the congruence problem is that of computing the congruence kernel
. In its modern form, the congruence problem is that of computing the congruence kernel 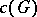 .
.
If 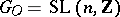 , where
, where  is the ring of integers, it was known already in the 19th century that the congruence problem has a negative solution for
is the ring of integers, it was known already in the 19th century that the congruence problem has a negative solution for 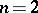 . For
. For 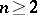 , it was proved in 1965 that every subgroup of finite index in
, it was proved in 1965 that every subgroup of finite index in 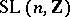 is a congruence subgroup (see [1]). After this, the congruence problem was solved [1] for
is a congruence subgroup (see [1]). After this, the congruence problem was solved [1] for 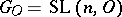 ,
, 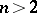 , and
, and 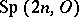 ,
, 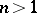 , where
, where  denotes the symplectic group. The results are as follows for these groups;
denotes the symplectic group. The results are as follows for these groups; 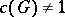 only for totally imaginary fields
only for totally imaginary fields 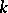 , in which case the congruence kernel is isomorphic to the (cyclic) group of roots of unity in
, in which case the congruence kernel is isomorphic to the (cyclic) group of roots of unity in 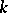 . It turned out that the same result holds for simply-connected Chevalley groups other than
. It turned out that the same result holds for simply-connected Chevalley groups other than  (see [3]). The condition of being simply connected is essential, because it follows from the strong approximation theorem (cf. Linear algebraic group) that the congruence kernel
(see [3]). The condition of being simply connected is essential, because it follows from the strong approximation theorem (cf. Linear algebraic group) that the congruence kernel 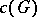 of a non-simply-connected semi-simple group
of a non-simply-connected semi-simple group 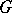 is infinite. For every non-semi-simple group
is infinite. For every non-semi-simple group 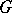 ,
, 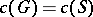 , where
, where 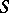 is a maximal semi-simple subgroup of
is a maximal semi-simple subgroup of 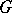 ; in particular,
; in particular, 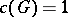 for a solvable group
for a solvable group 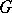 .
.
A more general form of the congruence problem is obtained by replacing 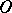 by the ring
by the ring
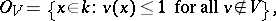 |
where 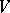 is any finite set of inequivalent norms of the field
is any finite set of inequivalent norms of the field 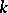 containing all Archimedean norms. In this situation, the congruence kernel, denoted by
containing all Archimedean norms. In this situation, the congruence kernel, denoted by  , depends in an essential way on
, depends in an essential way on 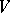 (see [4], [5]).
(see [4], [5]).
References
| [1] | H. Bass, J. Milnor, J.-P. Serre, "Solution of the congruence subgroup problem for 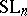 ( (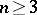 ) and ) and 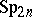 ( (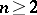 )" Publ. Math. IHES , 33 (1967) pp. 421–499 )" Publ. Math. IHES , 33 (1967) pp. 421–499 |
| [2] | J.-P. Serre, "Le problème des groupes de congruence pour 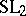 " Ann. of Math. , 92 (1970) pp. 489–527 " Ann. of Math. , 92 (1970) pp. 489–527 |
| [3] | H. Matsumoto, "Sur les sous-groupes arithmétiques des groupes semi-simples dépolyés" Ann. Sci. Ecole Norm. Sup. (4) , 2 (1969) pp. 1–62 |
| [4] | V.P. Platonov, "Algebraic groups" J. Soviet Math. , 4 : 5 (1975) pp. 463–482 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 11 (1974) pp. 5–37 |
| [5] | M. Raghunathan, "On the congruence subgroup problem" Publ. Math. IHES , 46 (1946) pp. 107–161 |
Comments
The congruence problem is usually called the congruence subgroup problem.
Congruence subgroup problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Congruence_subgroup_problem&oldid=21409