Normal subgroup
normal divisor, invariant subgroup
A subgroup 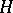 of a group
of a group  for which the left decomposition of
for which the left decomposition of 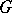 modulo
modulo 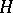 is the same as the right one; in other words, a subgroup such that for any element
is the same as the right one; in other words, a subgroup such that for any element 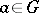 the cosets
the cosets 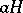 and
and 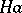 are the same (as sets). In this case one also says that
are the same (as sets). In this case one also says that 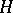 is normal in
is normal in 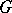 and writes
and writes 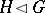 ; if also
; if also 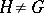 , one writes
, one writes 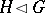 . A subgroup
. A subgroup 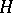 is normal in
is normal in 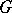 if and only if it contains all
if and only if it contains all 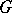 -conjugates of any of its elements (see Conjugate elements), that is
-conjugates of any of its elements (see Conjugate elements), that is 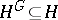 . A normal subgroup can also be defined as one that coincides with all its conjugates, as a consequence of which it is also known as a self-conjugate subgroup.
. A normal subgroup can also be defined as one that coincides with all its conjugates, as a consequence of which it is also known as a self-conjugate subgroup.
For any homomorphism 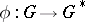 the set
the set 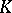 of elements of
of elements of 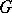 that are mapped to the unit element of
that are mapped to the unit element of 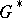 (the kernel of the homomorphism
(the kernel of the homomorphism 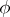 ) is a normal subgroup of
) is a normal subgroup of 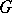 , and conversely, every normal subgroup of
, and conversely, every normal subgroup of 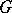 is the kernel of some homomorphism; in particular,
is the kernel of some homomorphism; in particular, 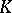 is the kernel of the canonical homomorphism onto the quotient group
is the kernel of the canonical homomorphism onto the quotient group 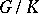 .
.
The intersection of any set of normal subgroups is normal, and the subgroup generated by any system of normal subgroups of 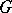 is normal in
is normal in 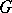 .
.
Comments
A subgroup 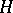 of a group
of a group 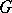 is normal if
is normal if 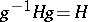 for all
for all 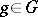 , or, equivalently, if the normalizer
, or, equivalently, if the normalizer 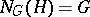 , cf. Normalizer of a subset. A normal subgroup is also called an invariant subgroup because it is invariant under the inner automorphisms
, cf. Normalizer of a subset. A normal subgroup is also called an invariant subgroup because it is invariant under the inner automorphisms 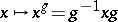 ,
, 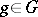 , of
, of 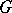 . A subgroup that is invariant under all automorphisms is called a fully-invariant subgroup or characteristic subgroup. A subgroup that is invariant under all endomorphisms is a fully-characteristic subgroup.
. A subgroup that is invariant under all automorphisms is called a fully-invariant subgroup or characteristic subgroup. A subgroup that is invariant under all endomorphisms is a fully-characteristic subgroup.
References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) pp. 26 |
| [a2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) pp. 5 |
| [a3] | A.G. Kurosh, "The theory of groups" , 1 , Chelsea (1955) pp. Chapt. III (Translated from Russian) |
Normal subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_subgroup&oldid=21397