Commutator subgroup

of a group, derived group, second term of the lower central series, of a group

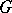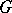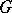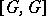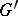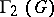The subgroup of the group generated by all commutators of the elements of (cf. Commutator). The commutator subgroup of is usually denoted by , or . The commutator subgroup is a fully-characteristic subgroup, and any subgroup containing the commutator subgroup is a normal subgroup. The quotient group with respect to some normal subgroup is Abelian if and only if this normal subgroup contains the commutator subgroup of the group.

The commutator ideal of a ring 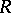is the ideal generated by all products 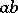, 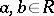; it is also called the square of 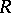and is denoted by 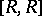or .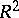

Both the above concepts are special cases of the notion of the commutator subgroup of a multi-operator -group 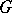, which is defined as the ideal generated by all commutators and all elements of the form

(*)

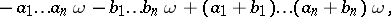where 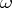is an -ary operation in and

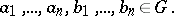Comments

In the case of a ring considered as an operator -group the commutators (of the underlying commutative group) are all zero, so that the commutator ideal is the ideal generated by all elements 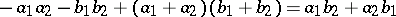. Hence 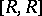is the ideal generated by all products .

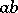More generally, in all three cases one defines the commutator group (ideal) 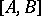of two -subgroups 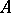and 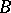as the ideal generated by all commutators 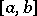, , 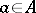, 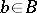and all elements (*) with , .

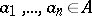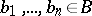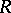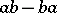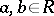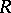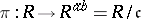In the case of a ring there is a second, different notion which also goes by the name of commutator ideal. It is the ideal generated by all commutators , . This one is universal for homomorphisms of into commutative rings. I.e. if is this ideal and is the natural projection, then for each homomorphism 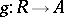into a commutative ring 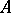there is a unique homomorphism 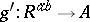such that 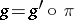( 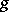factors uniquely through 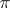). This is analogous to the property that for ordinary groups 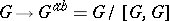is universal for mappings of 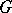into Abelian groups (cf. Universal problems).

References

[a1]	P.M. Cohn, "Algebra" , 2 , Wiley (1977)
[a2]	A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)