Transcendental extension
A field extension that is not algebraic (cf. Extension of a field). An extension 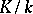 is transcendental if and only if the field
is transcendental if and only if the field  contains elements that are transcendental over
contains elements that are transcendental over 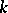 , that is, elements that are not roots of any non-zero polynomial with coefficients in
, that is, elements that are not roots of any non-zero polynomial with coefficients in 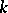 .
.
The elements of a set  are called algebraically independent over
are called algebraically independent over 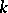 if for any finite set
if for any finite set 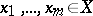 and any non-zero polynomial
and any non-zero polynomial  with coefficients in
with coefficients in 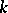 ,
,
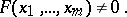 |
The elements of 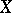 are transcendental over
are transcendental over 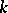 . If
. If  is a maximal set of algebraically independent elements over
is a maximal set of algebraically independent elements over  , then
, then 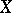 is called a transcendence basis of
is called a transcendence basis of 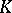 over
over 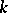 . The cardinality of
. The cardinality of  is called the transcendence degree of
is called the transcendence degree of  over
over 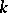 and is an invariant of the extension
and is an invariant of the extension 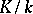 . For a tower of fields
. For a tower of fields 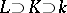 , the transcendence degree of
, the transcendence degree of 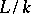 is equal to the sum of the transcendence degrees of
is equal to the sum of the transcendence degrees of 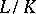 and
and 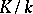 .
.
If all elements of a set  are algebraically independent over
are algebraically independent over 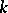 , then the extension
, then the extension 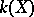 is called purely transcendental. In this case the field
is called purely transcendental. In this case the field 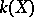 is isomorphic to the field of rational functions in the set of variables
is isomorphic to the field of rational functions in the set of variables  over
over  . Any field extension
. Any field extension 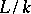 can be represented as a tower of extensions
can be represented as a tower of extensions  , where
, where 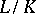 is an algebraic and
is an algebraic and 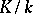 is a purely transcendental extension. If
is a purely transcendental extension. If 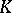 can be chosen so that
can be chosen so that 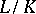 is a separable extension, then the extension
is a separable extension, then the extension 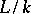 is called separably generated, and the transcendence basis of
is called separably generated, and the transcendence basis of  over
over 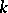 is called a separating basis. If
is called a separating basis. If  is separably generated over
is separably generated over 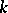 , then
, then 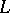 is separable over
is separable over 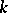 . In the case when the extension
. In the case when the extension 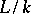 is finitely generated, the converse holds as well. By definition, an extension
is finitely generated, the converse holds as well. By definition, an extension  is separable if and only if any derivation (cf. Derivation in a ring) of
is separable if and only if any derivation (cf. Derivation in a ring) of  extends to
extends to 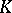 . Such an extension is uniquely determined for any derivation if and only if the extension
. Such an extension is uniquely determined for any derivation if and only if the extension  is algebraic.
is algebraic.
References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
| [2] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Springer (1988) pp. Chapt. 4–6 (Translated from French) |
Comments
The Noether normalization lemma says that if 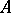 is an integral domain that is finitely generated as a ring over a field
is an integral domain that is finitely generated as a ring over a field 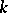 , then there exist
, then there exist 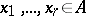 that are algebraically independent over
that are algebraically independent over 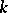 such that
such that 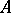 is integral over
is integral over 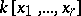 .
.
References
| [a1] | P.M. Cohn, "Algebra" , 1–2 , Wiley (1989) pp. Vol. 2, 350; Vol. 3, 168ff |
Transcendental extension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendental_extension&oldid=21155