Algebraically closed field

A field in which any polynomial of non-zero degree over has at least one root. In fact, it follows that for an algebraically closed field 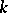each polynomial of degree over has exactly roots in , i.e. each irreducible polynomial from the ring of polynomials 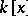is of degree one. A field is algebraically closed if and only if it has no proper algebraic extension (cf. Extension of a field). For any field , there exists a unique (up to isomorphism) algebraic extension of 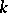that is algebraically closed; it is called the algebraic closure of 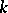and is usually denoted by . Any algebraically closed field containing contains a subfield isomorphic to .

The field of complex numbers is the algebraic closure of the field of real numbers. This is the fundamental theorem of algebra (cf. Algebra, fundamental theorem of).

References

[1]	O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975)
[2]	S. Lang, "Algebra" , Addison-Wesley (1974)