Darboux net invariants
From Encyclopedia of Mathematics
The expressions 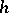 and
and 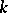 ,
,
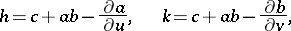 |
derived from the coefficients of the Laplace equation (in differential line geometry)
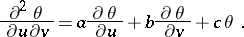 | (*) |
Equation (*) is satisfied by the homogeneous coordinates of a point  describing a conjugate net of lines
describing a conjugate net of lines  and
and  on a two-dimensional surface in an
on a two-dimensional surface in an  -dimensional projective space, where
-dimensional projective space, where 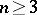 . It was shown by G. Darboux [1] that the Darboux invariants
. It was shown by G. Darboux [1] that the Darboux invariants 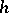 and
and 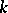 do not change their value when the normalization of the coordinates of the point
do not change their value when the normalization of the coordinates of the point  is changed. Special forms of conjugate nets are obtained by imposing some condition on the Darboux invariants.
is changed. Special forms of conjugate nets are obtained by imposing some condition on the Darboux invariants.
References
| [1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 2 , Gauthier-Villars (1889) |
| [2] | G. Tzitzeica, "Géométrie différentielle projective des réseaux" , Gauthier-Villars & Acad. Roumaine (1924) |
| [3] | S.P. Finikov, "Theorie der Kongruenzen" , Akademie Verlag (1959) (Translated from Russian) |
Comments
The expressions  and
and 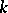 are more commonly referred to as the Darboux invariants of a net.
are more commonly referred to as the Darboux invariants of a net.
How to Cite This Entry:
Darboux net invariants. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_net_invariants&oldid=20844
Darboux net invariants. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_net_invariants&oldid=20844
This article was adapted from an original article by V.T. Bazylev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article