Cross product

crossed product, of a group and a ring

An associative ring defined as follows. Suppose one is given a mapping of a group into the isomorphism group of an associative ring with an identity, and a family

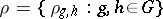of invertible elements of , satisfying the conditions

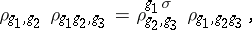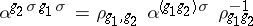for all 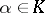and 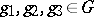. The family is called a factor system. Then the cross product of and with respect to the factor system and the mapping is the set of all formal finite sums of the form

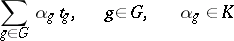(where the are symbols uniquely assigned to every element ), with binary operations defined by

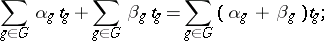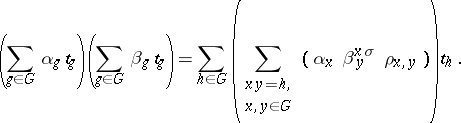This ring is denoted by ; the elements form a 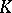-basis of it.

If maps 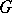onto the identity automorphism of , then 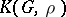is called a twisted or crossed group ring, and if, in addition, for all , then 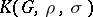is the group ring of 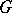over 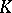(see Group algebra).

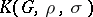Let be a field and a monomorphism. Then is a simple ring, being the cross product of the field with its Galois group.

References

[1]	S.K. Sehgal, "Topics in group rings" , M. Dekker (1978)
[2]	A.A. Bovdi, "Cross products of semi-groups and rings" Sibirsk. Mat. Zh. , 4 (1963) pp. 481–499 (In Russian)
[3]	A.E. Zalesskii, A.V. Mikhalev, "Group rings" J. Soviet Math. , 4 (1975) pp. 1–74 Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 2 (1973) pp. 5–118
[4]	D.S. Passman, "The algebraic structure of group rings" , Wiley (1977)

Comments

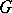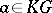In the defining relations for a factor system above , e.g., of course stands for the result of applying the automorphism to the element . If for all , then one obtains the skew group ring . Cross products arise naturally when dealing with extensions. Indeed, let be a normal subgroup of . Choose a set of representatives of in . Then every , the group algebra of 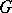, can be written as a unique sum , 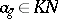. Now write

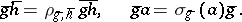Then the define a factor system (for the group 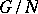and the ring relative to the set of automorphisms ) and

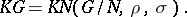Up to Brauer equivalence every central simple algebra is a cross product, but not every division algebra is isomorphic to a cross product. Two algebras over are Brauer equivalent if 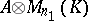is isomorphic to for suitable 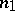and . Here 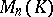is the algebra of 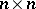matrices over . Cf. also Brauer group.