Sublattice
From Encyclopedia of Mathematics
A subset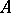 
of a lattice that is closed under the operations 
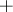and 
, i.e. a subset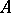 
such that 
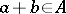and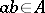 
for any 
and 
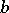from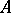 
. Therefore, a sublattice is a subalgebra of the lattice considered as a universal algebra with two binary operations. A sublattice 
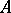is called convex if 
and 
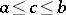imply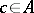 
. An example of a sublattice is any one-element subset of a lattice; other examples are: an ideal, a filter and an interval. All these sublattices are convex. Any subset in a chain is a sublattice of it (not necessarily convex). The sublattices of a given lattice, ordered by inclusion, form a lattice.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | L.A. Skornyakov, "Elements of lattice theory" , A. Hilger & Hindushtan Publ. Comp. (1977) (Translated from Russian) |
| [3] | G.I. Zhitomirskii, "Lattices of subsets" , Ordered sets and lattices , 7 , Saratov (1983) pp. 69–97 (In Russian) |
| [4] | G. Grätzer, "General lattice theory" , Birkhäuser (1978) (Original: Lattice theory. First concepts and distributive lattices. Freeman, 1978) |
How to Cite This Entry:
Sublattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sublattice&oldid=20292
Sublattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sublattice&oldid=20292
This article was adapted from an original article by T.S. Fofanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article