Semi-simple algebraic group
A connected linear algebraic group of positive dimension which contains only trivial solvable (or, equivalently, Abelian) connected closed normal subgroups. The quotient group of a connected non-solvable linear group by its radical is semi-simple.
A connected linear algebraic group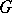 
of positive dimension is called simple (or quasi-simple) if it does not contain proper connected closed normal subgroups. The centre 
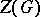of a simple group 
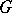is finite, and 
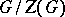is simple as an abstract group. An algebraic group 
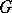is semi-simple if and only if 
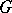is a product of simple connected closed normal subgroups.
If the ground field is the field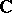 
of complex numbers, a semi-simple algebraic group is nothing but a semi-simple Lie group over 
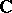(cf. Lie group, semi-simple). It turns out that the classification of semi-simple algebraic groups over an arbitrary algebraically closed field 
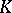is analogous to the case 
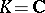, that is, a semi-simple algebraic group is determined up to isomorphism by its root system and a certain sublattice in the weight lattice that contains all the roots. More precisely, let 
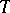be a maximal torus in the semi-simple algebraic group 
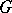and let 
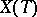be the character group of 
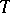, regarded as a lattice in the space 
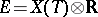. For a rational linear representation 
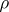of 
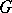, the group 
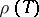is diagonalizable. Its eigenvalues, which are elements of 
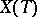, are called the weights of the representation 
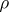. The non-zero weights of the adjoint representation 
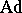are called the roots of 
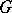. It turns out that the system 
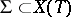of all roots of 
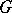is a root system in the space 
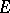, and that the irreducible components of the system 
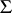are the root systems for the simple closed normal subgroups of 
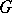. Furthermore, 
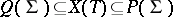, where 
is the lattice spanned by all roots and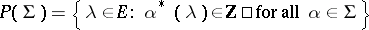 
is the weight lattice in the root system 
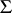. In the case 
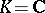the space 
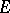can be naturally identified with a real subspace 
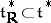, where 
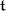is the Lie algebra of the torus 
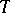, spanned by the differentials of all characters, while the lattices in 
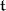dual to 
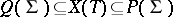coincide (up to a factor 
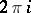) with 
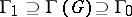(see Lie group, semi-simple).
The main classification theorem states that if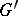 
is another semi-simple algebraic group, 
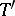its maximal torus, 
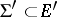a root system of 
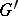, and if there is a linear mapping 
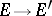giving an isomorphism between the root systems 
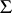and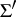 
and mapping 
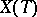onto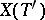 
, then 
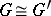(local isomorphism). Moreover, for any reduced root system 
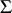and any lattice 
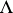satisfying the condition 
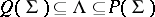there exists a semi-simple algebraic group 
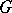such that 
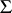is its root system with respect to the maximal torus 
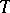, and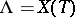 
.
The isogenies (in particular, all automorphisms, cf. Isogeny) of a semi-simple algebraic group have also been classified.
References
| [1] | R.G. Steinberg, "Lectures on Chevalley groups" , Yale Univ. Press (1968) |
| [2] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) |
Comments
References
| [a1] | T.A. Springer, "Linear algebraic groups" , Birkhäuser (1981) |
Semi-simple algebraic group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-simple_algebraic_group&oldid=19933