Cubic equation

An algebraic equation of degree three, i.e. an equation of the form

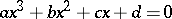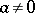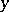where . Replacing in this equation by the new unknown defined by 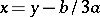, one brings the equation to the following simpler (canonical) form:

where

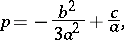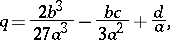and the solution to this equation may be obtained by using Cardano's formula (cf. Cardano formula); in other words, any cubic equation is solvable in radicals.

The cubic equation was first solved in the 16th century. At the beginning of that century, S. Ferro solved the equation 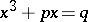, where 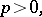, , 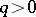but did not publish his solution. N. Tartaglia rediscovered Ferro's result; he also solved the equation 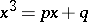(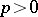, 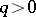), and announced without proof that the equation 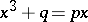(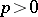, 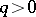) could be reduced to that form. Tartaglia communicated his results to G. Cardano, who published the solution of the general cubic equation in 1545.

References

[1]	A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian)

Comments

The history is treated in [a2], where Cardano's name (wrongly) occurs as Cardan (Chapt. 12).

References

[a1]	B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German)
[a2]	W.W. Rouse Ball, "A short account of the history of mathematics" , Dover, reprint (1960) pp. 123–125