Ferrari method
A method for reducing the solution of an equation of degree 4 to the solution of one cubic and two quadratic equations; it was discovered by L. Ferrari (published in 1545).
The Ferrari method for the equation
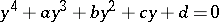 |
consists in the following. By the substitution 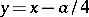 the given equation can be reduced to
the given equation can be reduced to
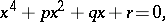 | (1) |
which contains no term in 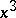 . If one introduces an auxiliary parameter
. If one introduces an auxiliary parameter 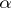 , the left-hand side of (1) can be written as
, the left-hand side of (1) can be written as
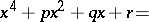 | (2) |
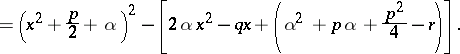 |
One then chooses a value of 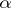 such that the expression in square brackets is a perfect square. For this the discriminant of the quadratic trinomial must vanish. This gives a cubic equation for
such that the expression in square brackets is a perfect square. For this the discriminant of the quadratic trinomial must vanish. This gives a cubic equation for 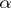 ,
,
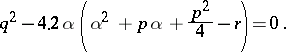 |
Let 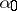 be one of the roots of this equation. For
be one of the roots of this equation. For 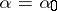 the polynomial in square brackets in (2) has one double root,
the polynomial in square brackets in (2) has one double root,
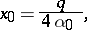 |
which leads to the equation
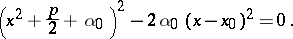 |
This equation of degree 4 splits into two quadratic equations. The roots of these equations are also the roots of (1).
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Ferrari method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ferrari_method&oldid=19674