Cremona transformation

A birational transformation of a projective space 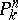, , 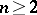over a field 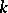. Birational transformations of the plane and of three-dimensional space were systematically studied (from 1863 on) by L. Cremona. The group of Cremona transformations is also named after him — the Cremona group, and is denoted by .

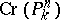The simplest examples of Cremona transformations which are not projective transformations are quadratic birational transformations of the plane. In non-homogeneous coordinates 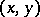they may be expressed as linear-fractional transformations

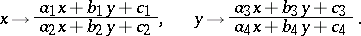Among these transformations, special consideration is given to the standard quadratic transformation :

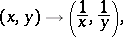or, in homogeneous coordinates,

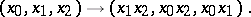This transformation is an isomorphism off the coordinate axes:

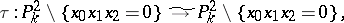it has three fundamental points (points at which is it undefined) 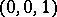, 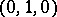and , and 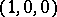maps each coordinate axis onto the unique fundamental point not contained in that axis.

By Noether's theorem (see Cremona group), if 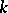is an algebraically closed field, each Cremona transformation of the plane 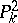can be expressed as a composition of quadratic transformations.

An important place in the theory of Cremona transformations is occupied by certain special classes of transformations, in particular — Geiser involutions and Bertini involutions (see [1]). A Geiser involution 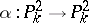is defined by a linear system of curves of degree 8 on 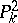, which pass with multiplicity 3 through 7 points in general position. A Bertini involution 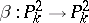is defined by a linear system of curves of degree 17 on 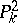, which pass with multiplicity 6 through 8 points in general position.

A Cremona transformation of the form

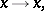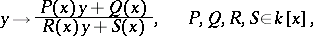is called a de Jonquières transformation. De Jonquières transformations are most naturally interpreted as birational transformations of the quadric 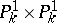which preserve projection onto one of the factors. One can then restate Noether's theorem as follows: The group 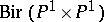of birational automorphisms of the quadric is generated by an involution 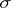and by the de Jonquières transformations, where 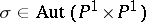is the automorphism defined by permutation of factors.

Any biregular automorphism of the affine space 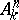in 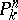may be extended to a Cremona transformation of 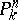, so that 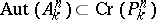. When 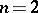the group 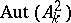is generated by the subgroup of affine transformations and the subgroup of transformations of the form

(*)

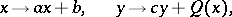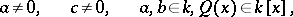moreover, it is the amalgamated product of these subgroups [5]. The structure of the group 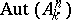, , 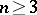is not known. In general, up to the present time (1987) no significant results have been obtained concerning Cremona transformations for dimensions .

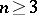References

[1]	H.P. Hudson, "Cremona transformations in plane and space" , Cambridge Univ. Press (1927)
[2]	L. Godeaux, "Les transformations birationelles du plan" , Gauthier-Villars (1927)
[3]	A.B. Coble, "Algebraic geometry and theta functions" , Amer. Math. Soc. (1929)
[4]	M. Nagata, "On rational surfaces II" Mem. Coll. Sci. Univ. Kyoto , 33 (1960) pp. 271–393
[5]	I.R. Shafarevich, "On some infinitedimensional groups" Rend. di Math , 25 (1966) pp. 208–212

Comments

The fact that 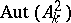is the amalgamated product of the subgroup of affine transformations (cf. Affine transformation) with that of the transformations (*) was first proved (for 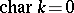) by H.W.E. Jung [a1]; the case of arbitrary ground field was proved by W. van der Kulk [a2].

References

[a1]	H.W.E. Jung, "Ueber ganze birationale Transformationen der Ebene" J. Reine Angew. Math. , 184 (1942) pp. 161–174
[a2]	W. van der Kulk, "On polynomial rings in two variables" Nieuw Arch. Wiskunde , 1 (1953) pp. 33–41