Albanese variety

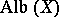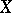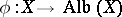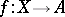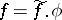An Abelian variety canonically attached to an algebraic variety , which is the solution of the following universal problem: There exists a morphism such that any morphism into an Abelian variety factors into a product , where 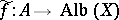(so named in honour of G. Albanese). If 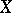is a complete non-singular variety over the field of complex numbers, the Albanese variety can be described as follows. Let 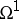be the space of everywhere-regular differential forms of degree 1 on . Each one-dimensional cycle 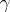of the topological space 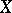determines a linear functi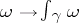on on . The image of the mapping 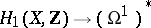thus obtained is a lattice 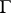in 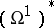, and the quotient space 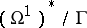coincides with the Albanese variety of 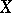. From the algebraic point of view, an Albanese variety may be considered as a method of defining an algebraic structure on some quotient group of the group 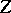of zero-dimensional cycles of degree 0 on 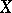. If 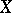is a non-singular complete algebraic curve, both its Picard variety and its Albanese variety are called its Jacobi variety. If the ground field has characteristic zero, then the equalities

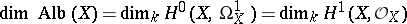are valid. The number 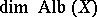is called the irregularity of the variety 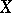. If the field has finite characteristic, the inequalities

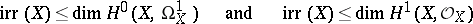hold. If the ground field has positive characteristics it can happen that

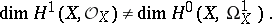The Albanese variety is dual to the Picard variety.

References

[1]	M. Baldassarri, "Algebraic varieties" , Springer (1956)
[2]	S. Lang, "Abelian varieties" , Springer (1983)