Commutative group scheme

A group scheme 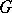over a basis scheme 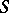, the value of which on any 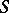-scheme is an Abelian group. Examples of commutative group schemes are Abelian schemes and algebraic tori (cf. Algebraic torus; Abelian scheme). A generalization of algebraic tori in the framework of the theory of group schemes is the following notion. A commutative group scheme is said to be a group scheme of multiplicative type if for any point 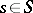there is an open neighbourhood 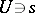and and an absolutely-flat quasi-compact morphism 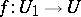such that the commutative group scheme 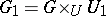is diagonalizable over 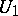. Here, a diagonalizable group scheme is a group scheme of the form

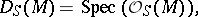where 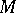is an Abelian group and 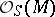is its group algebra with coefficients in the structure sheaf 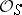of the scheme 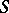. In the case when 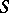is the spectrum of an algebraically closed field, this notion reduces to that of a diagonalizable group. If 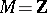is the additive group of integers, then 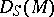coincides with the multiplicative group scheme .

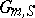Let 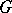be a group scheme over 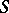whose fibre over the point 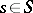is a group scheme of multiplicative type over the residue class field 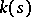. Then there is a neighbourhood 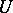of such that is a group scheme of multiplicative type over 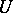(Grothendieck's rigidity theorem).

The structure of commutative group schemes has been studied in the case when the basis scheme 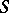is the spectrum of a field 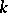, and the commutative group scheme 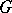is of finite type over 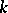. In this case the commutative group scheme contains a maximal invariant affine group subscheme, the quotient with respect to which is an Abelian variety (a structure theorem of Chevalley). Any affine commutative group scheme 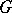of such a type has a maximal invariant group subscheme of multiplicative type, the quotient with respect to which is a unipotent group. If the field 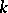is perfect, then 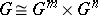, where 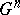is a maximal unipotent subgroup of .

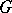References

[1]	J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)
[2]	M. Demazure, A. Grothendieck, "Schémas en groupes II" , Lect. notes in math. , 152 , Springer (1970)
[3]	M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson (1970)
[4]	F. Oort, "Commutative group schemes" , Lect. notes in math. , 15 , Springer (1966)
[5]	W. Waterhouse, "Introduction to affine group schemes" , Springer (1979)

Comments

A group scheme over a scheme 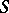is an 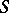-scheme such that 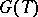is a group for any 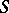-scheme 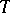. If is an Abelian, or commutative, group for all such 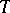, then 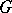is called a commutative group scheme.

The multiplicative group scheme 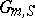takes the value 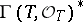, the group of invertible elements of the ring of functions on for each 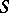-scheme 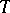. The additive group scheme 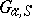takes the values 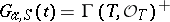, the underlying additive group of 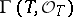. A group scheme over 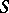can equivalently be defined as a group object in the category of -schemes.

References

[a1]	J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)