Zariski topology

on an affine space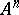

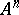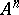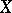The topology defined on by taking the closed sets to be the algebraic subvarieties of . If is an affine algebraic variety (see Affine algebraic set) in , the induced topology on 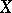is also known as the Zariski topology. In a similar manner one defines the Zariski topology of the affine scheme 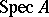of a ring 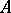(sometimes called the spectral topology) — the closed sets are all the sets

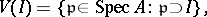where 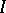is an ideal of .

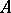The Zariski topology was first introduced by O. Zariski [1], as a topology on the set of valuations of an algebraic function field. Though, in general, the Zariski topology is not separable, many constructions of algebraic topology carry over to it [2]. An affine scheme endowed with the Zariski topology is quasi-compact.

The topology most naturally defined on an arbitrary scheme is also called the Zariski topology in order to distinguish between it and the étale topology, or, if the variety 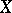is defined over the field 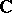, between it and the topology of an analytic space on the set of complex-valued points of .

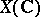References

[1]	O. Zariski, "The compactness of the Riemann manifold of an abstract field of algebraic functions" Bull. Amer. Math. Soc. , 50 : 10 (1944) pp. 683–691
[2]	J.-P. Serre, , Fibre spaces and their applications , Moscow (1958) pp. 372–450 (In Russian; translated from French)

References

[a1]	R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2