Thermodynamics, mathematical problems in
Problems connected with the research on general properties of macroscopic systems in states of thermodynamical equilibrium, and the transition processes between those states.
The mathematical machinery of macroscopic thermodynamics arises from the so-called principles of thermodynamics. According to the zero-th principle, a thermodynamical system must admit a stable equilibrium state, which is unique in the thermodynamical sense, determined by a fixation of the external conditions acting on the system. The first principle — the law of conservation and transformation of energy — for a statistically infinitesimal change in the state parameters of the system (that is, for a sufficiently-slow change from one equilibrium state to another) relates the heat effect of this process 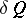 to the change in internal energy
to the change in internal energy 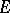 of the system and the quantity of work
of the system and the quantity of work 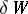 produced by the system. If one takes, as a clear and fairly simple example, a gas-type system with a fixed number of particles, then its states can be determined by three parameters, such as, for example, its temperature
produced by the system. If one takes, as a clear and fairly simple example, a gas-type system with a fixed number of particles, then its states can be determined by three parameters, such as, for example, its temperature 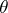 , volume
, volume 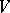 and number of particles
and number of particles 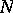 (other variants are also possible). Then the work associated with a process of expansion is
(other variants are also possible). Then the work associated with a process of expansion is 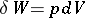 , where
, where 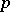 is the pressure of the gas, and the first principle determines the energy balance
is the pressure of the gas, and the first principle determines the energy balance
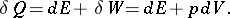 | (1) |
From the second principle of thermodynamics for quasi-static processes: the existence of entropy as a single-valued function of thermodynamical states with complete differential
 | (2) |
there follows a system of equations for the specific energy 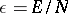 as a function of
as a function of 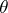 and the specific volume
and the specific volume  :
:
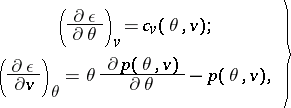 | (3) |
which define it up to a constant 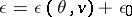 , and define the total internal energy up to an additive constant
, and define the total internal energy up to an additive constant 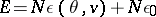 . The system of equations for the specific entropy
. The system of equations for the specific entropy
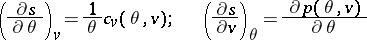 | (4) |
defines 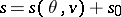 up to a constant (and the complete entropy
up to a constant (and the complete entropy 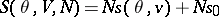 up to an additive constant
up to an additive constant 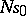 ).
).
The remaining thermodynamical characteristics of the system, a thermodynamic potential, etc., can be defined in terms of solutions to these equations, using mathematical operations no more complicated than differentiation.
To solve equations (3) and (4) the thermodynamical system must be fixed. This concretization of a system usually involves fixing the state equations (a single equation in the simplified case above) 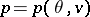 , and the caloric equation of state — the thermal capacity
, and the caloric equation of state — the thermal capacity 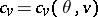 , which determine the macroscopic reaction of the system with respect to a change of the external parameters (volume in the above case) and with respect to its temperature. The constant
, which determine the macroscopic reaction of the system with respect to a change of the external parameters (volume in the above case) and with respect to its temperature. The constant 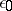 must be chosen in accordance with the origin of the energy reference system. The entropy constant, which is necessary when solving a series of concrete problems, is determined using the third principle of thermodynamics, which appears in Planck's formulation as a supplementary condition to the system of equations (4):
must be chosen in accordance with the origin of the energy reference system. The entropy constant, which is necessary when solving a series of concrete problems, is determined using the third principle of thermodynamics, which appears in Planck's formulation as a supplementary condition to the system of equations (4):
 | (5) |
The formulation of the problem introduced above can be referred to as direct. There are various possible formulations converse to this one.
For investigating low-temperature problems, and in a series of other problems, one also uses a different formulation: According to the first equations for  and
and  and the third principle, one has:
and the third principle, one has:
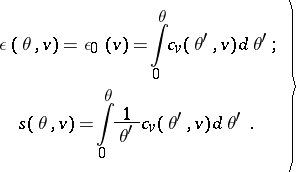 | (6) |
To perform these calculations, one must fix the caloric equations, that is,  , and the specific energy of the initial state of the system
, and the specific energy of the initial state of the system 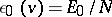 . This quantity cannot be measured directly, as a rule. It can be fixed in any given model, or obtained indirectly from the state equations introduced above.
. This quantity cannot be measured directly, as a rule. It can be fixed in any given model, or obtained indirectly from the state equations introduced above.
The presence of external fields (electrostatic, magnetic, etc.) can be taken into account in the scheme above (at the cost of increasing the number of equations of types (3) and (4)). But this can be achieved most simply by calculating the change in the free energy 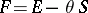 as the field
as the field  increases from zero to the given size. The reaction of the system to this increase must be given in terms of a corresponding state equation
increases from zero to the given size. The reaction of the system to this increase must be given in terms of a corresponding state equation 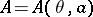 such that the work done by the system under a quasi-static change
such that the work done by the system under a quasi-static change 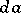 in the field is given by
in the field is given by 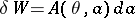 . Thus, by (1) and (2),
. Thus, by (1) and (2),
 | (7) |
and the required value is (omitting all parameters except 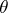 and
and  )
)
 | (8) |
The change in the thermodynamical characteristic, associated with an increase in the field  , is obtained using a corresponding differentiation of (8), together with simple algebraic operations.
, is obtained using a corresponding differentiation of (8), together with simple algebraic operations.
In view of the fact that it is possible to give a thermodynamical system in terms of convenient formulas for 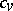 ,
, 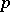 ,
,  , etc., only for simplified models, the computation of real thermodynamic effects (that is, the solution of problems of technical thermodynamics) is carried out by numerical methods, auxiliary tables, etc.
, etc., only for simplified models, the computation of real thermodynamic effects (that is, the solution of problems of technical thermodynamics) is carried out by numerical methods, auxiliary tables, etc.
Investigations have been conducted into the peculiarities of a thermodynamical system close to a critical point (or in a second-order phase transition, in view of certain similarities it has close to critical phenomena). The behaviour of a series of thermodynamical characteristics near such a point is characterized by powers of the dimensionless deviation of the temperature from the critical temperature: 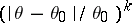 . The parameters
. The parameters 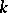 are called the critical indices, and by methods of macroscopic thermodynamics (sometimes in the context of general schemes of equilibrium statistical mechanics) a series of universal relations for them (usually in the form of inequalities) (3) have been established.
are called the critical indices, and by methods of macroscopic thermodynamics (sometimes in the context of general schemes of equilibrium statistical mechanics) a series of universal relations for them (usually in the form of inequalities) (3) have been established.
The mathematical problems of the thermodynamical theory of transfer phenomena are not complicated (cf. [1], [4]). They generally consist of the study of a system of linear relationships, relating the flow 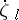 to the deviation of a macroscopic quantity
to the deviation of a macroscopic quantity  from its equilibrium value. The coefficients for
from its equilibrium value. The coefficients for  are subject to certain symmetry conditions, and are expressed in terms of the actual transfer coefficients. If one treats these equations as time equations for
are subject to certain symmetry conditions, and are expressed in terms of the actual transfer coefficients. If one treats these equations as time equations for 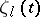 (in a fairly large time scale), then the solution of this system (which is possible in general form only in rare cases) determines, in the semi-phenomenological theory, the character of relaxation of the system towards a state of equilibrium.
(in a fairly large time scale), then the solution of this system (which is possible in general form only in rare cases) determines, in the semi-phenomenological theory, the character of relaxation of the system towards a state of equilibrium.
References
| [1] | I.P. Bazarov, "Thermodynamics" , Moscow (1983) (In Russian) |
| [2] | R. Kubo, "Thermodynamics" , North-Holland (1968) |
| [3] | H.E. Stanley, "Introduction to phase transitions and critical phenomena" , Oxford Univ. Press (1971) |
| [4] | S.R. de Groot, P. Mazur, "Non-equilibrium thermodynamics" , North-Holland (1962) |
Comments
References
| [a1] | S. Flügge (ed.) , Handbuch der Physik , Encycl. Physics , 12. Thermodynamics of gases , Springer (1958) |
| [a2] | J. Serrin (ed.) , New perspectives in thermodynamics , Springer (1986) |
Thermodynamics, mathematical problems in. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thermodynamics,_mathematical_problems_in&oldid=48962