Super-space
A vector space 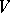 over a field
over a field 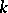 endowed with a
endowed with a 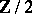 -grading
-grading  . The elements of the spaces
. The elements of the spaces 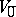 and
and 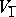 are said to be even and odd, respectively; for
are said to be even and odd, respectively; for 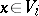 , the parity
, the parity 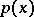 is defined to be
is defined to be 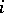
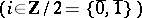 . Each super-space
. Each super-space 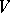 has associated to it another super-space
has associated to it another super-space  such that
such that 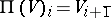
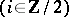 . The pair
. The pair 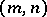 , where
, where 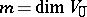 ,
, 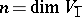 , is called the dimension of the super-space
, is called the dimension of the super-space  . The field
. The field 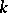 is usually considered as a super-space of dimension
is usually considered as a super-space of dimension 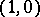 .
.
For two super-spaces 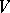 and
and 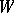 , the structure of a super-space on the spaces
, the structure of a super-space on the spaces 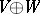 ,
, 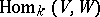 ,
, 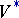 , etc., is defined naturally. In particular, a linear mapping
, etc., is defined naturally. In particular, a linear mapping 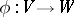 is even if
is even if 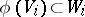 , and odd if
, and odd if 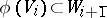 . A homogeneous bilinear form
. A homogeneous bilinear form 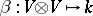 is said to be symmetric if
is said to be symmetric if
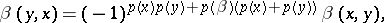 |
and skew-symmetric if
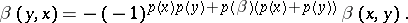 |
All these concepts apply equally to 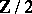 -graded free modules
-graded free modules 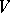 over an arbitrary commutative superalgebra
over an arbitrary commutative superalgebra 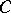 . The basis in
. The basis in 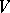 is usually selected so that its first vectors are even and its last ones odd. Any endomorphism
is usually selected so that its first vectors are even and its last ones odd. Any endomorphism 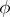 of the module
of the module 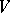 is denoted in this basis by a block matrix
is denoted in this basis by a block matrix
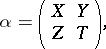 |
where 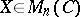 ,
, 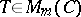 , such that if
, such that if 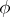 is even, then
is even, then 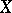 and
and 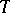 consist of even elements and
consist of even elements and 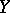 and
and 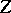 consist of odd elements, whereas if
consist of odd elements, whereas if 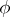 is odd, then
is odd, then 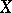 and
and 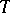 consist of odd elements and
consist of odd elements and 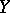 and
and 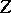 consist of even elements (in the former case the matrix
consist of even elements (in the former case the matrix 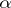 is even, in the latter, odd).
is even, in the latter, odd).
References
| [1] | F.A. Berezin, "Introduction to superanalysis" , Reidel (1987) (Translated from Russian) |
| [2] | D.A. Leites (ed.) , Seminar on super-manifolds , Kluwer (1990) |
Comments
References
| [a1] | F.A. Berezin, M.A. Shubin, "The Schrödinger equation" , Kluwer (1991) (Translated from Russian) (Supplement 3: D.A. Leites, Quantization and supermanifolds) |
Super-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Super-space&oldid=48910