Stochastic point process
point process
A stochastic process corresponding to a sequence of random variables  ,
,  , on the real line
, on the real line  . Each value
. Each value  corresponds to a random variable
corresponds to a random variable  called its multiplicity. In queueing theory a stochastic point process is generated by the moments of arrivals for service, in biology by the moments of impulses in nerve fibres, etc.
called its multiplicity. In queueing theory a stochastic point process is generated by the moments of arrivals for service, in biology by the moments of impulses in nerve fibres, etc.
The number  of all points
of all points  is called the counting process,
is called the counting process,  , where
, where  is a martingale and
is a martingale and 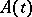 is the compensator with respect to the
is the compensator with respect to the 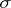 -fields
-fields  generated by the random points
generated by the random points  . Many important problems can be solved in terms of properties of the compensator
. Many important problems can be solved in terms of properties of the compensator  .
.
Let 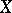 be a complete separable metric space,
be a complete separable metric space,  the class of bounded Borel sets
the class of bounded Borel sets 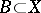 ,
,  the set of all measures that take integral values,
the set of all measures that take integral values,  , and
, and  the minimal
the minimal  -field generated by the subsets of measures
-field generated by the subsets of measures 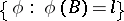 for
for 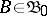 and
and 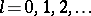 . Specifying a probability measure
. Specifying a probability measure 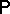 in the measurable space
in the measurable space 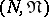 determines a stochastic point process
determines a stochastic point process 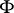 with state space
with state space 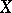 whose realizations are integer-valued measures on
whose realizations are integer-valued measures on 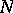 . The values
. The values  for which
for which 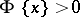 are called the points of
are called the points of 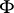 . The quantity
. The quantity  is equal to the sum of the multiplicities of the points of
is equal to the sum of the multiplicities of the points of 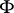 that lie in
that lie in 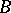 .
. 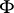 is called simple if
is called simple if 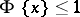 for all
for all 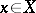 and ordinary if, for all
and ordinary if, for all 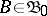 and
and  , there is a partition
, there is a partition  of
of  such that
such that
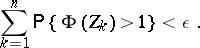 |
Ordinary stochastic point processes are simple. An important role is played by the factorial moment measures
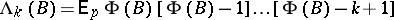 |
and their extensions (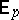 is the mathematical expectation and
is the mathematical expectation and  is called the measure of intensity). If
is called the measure of intensity). If 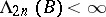 , then
, then
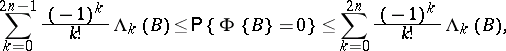 |
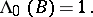 |
A special role in the theory of stochastic point processes is played by Poisson stochastic point processes 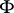 , for which: a) the values of
, for which: a) the values of 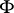 on disjoint
on disjoint 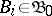 are mutually-independent random variables (the property of absence of after-effect); and b)
are mutually-independent random variables (the property of absence of after-effect); and b)
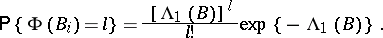 |
For a simple stochastic point process,
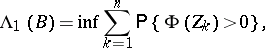 | (*) |
where the infimum is taken over all partitions 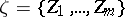 of
of 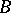 . The relation (*) makes it possible to find explicit expressions for the measure of intensity for many classes of stochastic point processes generated by stochastic processes or random fields.
. The relation (*) makes it possible to find explicit expressions for the measure of intensity for many classes of stochastic point processes generated by stochastic processes or random fields.
A generalization of stochastic point processes are the so-called marked stochastic point processes, in which marks  from some measurable space
from some measurable space 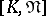 are assigned to points
are assigned to points  with
with 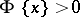 . The service times in a queueing system can be regarded as marks.
. The service times in a queueing system can be regarded as marks.
In the theory of stochastic point processes, an important role is played by relations connecting, in a special way, given conditional probabilities of distinct events (Palm probabilities). Limit theorems have been obtained for superposition (summation), thinning out and other operations on sequences of stochastic point processes. Various generalizations of Poisson stochastic point processes are widely used in applications.
References
| [1] | A.Ya. Khinchin, "Mathematical methods in the theory of queueing" , Griffin (1960) (Translated from Russian) |
| [2] | D.R. Cox, V. Isham, "Point processes" , Chapman & Hall (1980) |
| [3] | J. Kerstan, K. Matthes, J. Mecke, "Infinitely divisible point processes" , Wiley (1978) (Translated from German) |
| [4] | Yu.K. Belyaev, "Elements of the general theory of point processes" (Appendix to Russian translation of: H. Cramér, M. Leadbetter, Stationary and related stochastic processes, Wiley, 1967) |
| [5] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , II. Applications , Springer (1978) (Translated from Russian) |
| [6] | M. Jacobson, "Statistical analysis of counting processes" , Lect. notes in statistics , 12 , Springer (1982) |
Comments
Let  ,
, 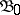 be as above; let
be as above; let 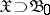 be the Borel field of
be the Borel field of  . Let
. Let  be the collection of all Borel measures on
be the collection of all Borel measures on 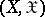 . For each
. For each 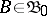 ,
,  defines a mapping
defines a mapping 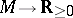 , and
, and  is the
is the 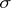 -field generated by those mappings, i.e. the smallest
-field generated by those mappings, i.e. the smallest 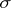 -field making all these mappings measurable. The integral-valued elements of
-field making all these mappings measurable. The integral-valued elements of  form the subspace
form the subspace 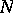 and
and 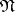 is the induced
is the induced 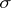 -field on
-field on 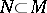 .
.
A random measure on  is simply a probability measure on
is simply a probability measure on  or, equivalently, a measurable mapping
or, equivalently, a measurable mapping  of some abstract probability space
of some abstract probability space 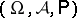 into
into 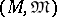 . A point process is the special case that
. A point process is the special case that 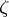 takes its values in
takes its values in 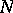 .
.
An element  is simple if
is simple if 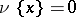 or
or 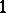 for all
for all  . A simple point process is one that takes its values in the subspace of
. A simple point process is one that takes its values in the subspace of  consisting of the simple measures.
consisting of the simple measures.
Each 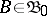 defines a function
defines a function 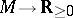 ,
, 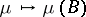 , and, hence, gives a random measure
, and, hence, gives a random measure 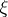 , a random variable which will be denoted by
, a random variable which will be denoted by 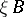 . One can think of a random measure in two ways: a collection of measures (on
. One can think of a random measure in two ways: a collection of measures (on 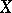 )
) 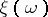 parametrized by a probability space
parametrized by a probability space 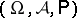 or a collection of random variables
or a collection of random variables 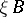 (on
(on  or on
or on 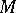 ) indexed by
) indexed by 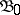 , depending on which part of the mapping
, depending on which part of the mapping 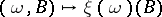 one focuses on.
one focuses on.
More generally, for each bounded continuous function 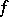 on
on 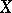 one has the random variable
one has the random variable 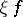 defined by
defined by
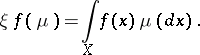 |
For each random measure 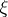 one defines the Palm distributions of
one defines the Palm distributions of 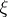 . For a simple point process
. For a simple point process 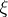 the Palm distribution
the Palm distribution 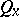 can be thought of as the conditional distribution of
can be thought of as the conditional distribution of 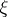 given that
given that 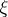 has an atom at
has an atom at 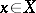 . Palm distributions are of great importance in random measure theory and have applications to queueing theory, branching processes, regenerative sets, stochastic geometry, statistical mechanics, and insurance mathematics (the last, via doubly stochastic Poisson processes, also called Cox processes, which are Poisson processes with stochastic variation in the intensity).
. Palm distributions are of great importance in random measure theory and have applications to queueing theory, branching processes, regenerative sets, stochastic geometry, statistical mechanics, and insurance mathematics (the last, via doubly stochastic Poisson processes, also called Cox processes, which are Poisson processes with stochastic variation in the intensity).
The Palm distribution of a random measure is obtained by disintegrating its Campbell measure on 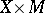 , which is given by
, which is given by
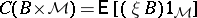 |
for 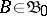 ,
, 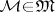 , where
, where 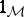 is the indicator function of
is the indicator function of 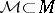 , the function
, the function 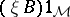 is the (pointwise) product of the two function
is the (pointwise) product of the two function 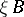 and
and 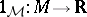 and
and 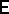 stands for expectation.
stands for expectation.
Disintegration of a measure is much related to conditional distributions (cf. Conditional distribution). Given two measurable spaces 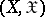 and
and 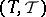 , a kernel, also called a Markov kernel, from
, a kernel, also called a Markov kernel, from 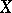 to
to 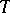 is a mapping
is a mapping 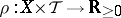 such that
such that 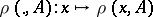 is measurable on
is measurable on 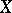 for all
for all 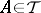 and such that
and such that 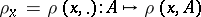 is a
is a 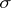 -finite measure on
-finite measure on 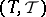 for all
for all 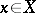 .
.
Given a 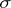 -finite measure
-finite measure 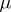 on the product space
on the product space 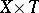 , a disintegration of
, a disintegration of 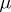 consists of a
consists of a 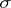 -finite measure
-finite measure  on
on 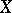 and a kernel
and a kernel 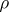 from
from 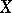 to
to 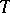 such that
such that 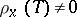
 -almost everywhere and such that for all
-almost everywhere and such that for all 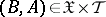 ,
,
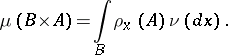 | (a1) |
It follows that for every measurable function 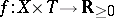 ,
,
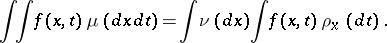 | (a2) |
The inverse operation is called mixing. Given  and
and 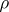 , the measure (a1) is called the mixture of the
, the measure (a1) is called the mixture of the 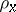 with respect to
with respect to  (and (a2) could be called the Fubini formula for mixture measures).
(and (a2) could be called the Fubini formula for mixture measures).
A disintegration exists for a 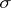 -finite
-finite 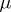 if
if  is Polish Borel. This reduces to a matter of conditional distributions. The measure
is Polish Borel. This reduces to a matter of conditional distributions. The measure  is unique up to equivalence, and
is unique up to equivalence, and 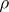 is unique up to a measurable renormalization
is unique up to a measurable renormalization  -almost everywhere. More generally one studies disintegration (or decomposition into slices) of a measure
-almost everywhere. More generally one studies disintegration (or decomposition into slices) of a measure 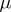 on a space
on a space 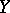 relative to any mapping
relative to any mapping 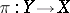 (instead of the projection
(instead of the projection 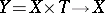 , cf. [a11], [a12]).
, cf. [a11], [a12]).
For each bounded continuous function 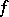 , let
, let 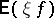 be the expectation of the random variable
be the expectation of the random variable 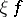 and let
and let 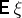 be the measure
be the measure 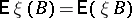 on
on 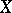 . Then, using (a2), the disintegration of the Campbell measure
. Then, using (a2), the disintegration of the Campbell measure 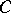 on
on 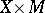 yields the measure
yields the measure 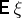 on
on 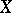 and, if
and, if 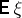 is
is 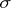 -finite, the
-finite, the 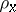 can be normalized
can be normalized 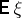 -almost everywhere to probability measures
-almost everywhere to probability measures 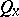 on
on 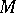 to give
to give
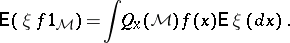 |
The 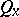 are the Palm distributions (Palm probabilities) of
are the Palm distributions (Palm probabilities) of 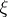 . Equivalently, as a function of
. Equivalently, as a function of  ,
, 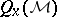 for
for 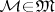 is
is 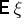 -almost everywhere the Radon–Nikodým derivative (cf. Radon–Nikodým theorem) of the measure
-almost everywhere the Radon–Nikodým derivative (cf. Radon–Nikodým theorem) of the measure 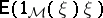 on
on 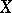 with respect to
with respect to 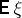 . Here
. Here  is the random measure
is the random measure 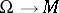 ,
,
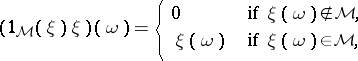 |
i.e. the trace of 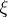 on
on 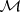 .
.
References
| [a1] | A.A. Borovkov, "Stochastic processes in queueing theory" , Springer (1976) (Translated from Russian) |
| [a2] | P.A.W. Lewis (ed.) , Stochastic point processes: statistical analysis theory and applications , Wiley (Interscience) (1972) |
| [a3] | V.K. Murthy, "The general point process" , Addison-Wesley (1974) |
| [a4] | D.C. Snyder, "Random point processes" , Wiley (1975) |
| [a5] | D.J. Daley, D. Vere-Jones, "An introduction to the theory of point processes" , Springer (1978) |
| [a6] | F. Baccelli, P. Brémaud, "Palm probabilities and stationary queues" , Lect. notes in statistics , 41 , Springer (1987) |
| [a7] | P. Brémaud, "Point processes and queues - Martingale dynamics" , Springer (1981) |
| [a8] | J. Neveu, "Processus ponctuels" J. Hoffmann-Jørgensen (ed.) T.M. Liggett (ed.) J. Neveu (ed.) , Ecole d'été de St. Flour VI 1976 , Lect. notes in math. , 598 , Springer (1977) pp. 250–448 |
| [a9] | O. Kallenberg, "Random measures" , Akademie Verlag & Acad. Press (1986) |
| [a10] | J. Grandell, "Doubly stochastic Poisson processes" , Springer (1976) |
| [a11] | H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart & Winston (1972) (Translated from German) |
| [a12] | N. Bourbaki, "Intégration" , Eléments de mathématiques , Hermann (1967) pp. Chapt. 5: Intégration des mesures, §6.6 |
| [a13] | N. Bourbaki, "Intégration" , Eléments de mathématiques , Hermann (1959) pp. Chapt. 6: Intégration vectorielle, §3 |
Stochastic point process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_point_process&oldid=48854