Similarity region
similar region
A generally used abbreviation of the term "critical region similar to a sample space" as used in mathematical statistics for a critical region with non-randomized similarity of a statistical test.
Let 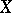 be a random variable taking values in a sample space
be a random variable taking values in a sample space 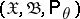 ,
, 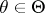 , and consider testing the compound hypothesis
, and consider testing the compound hypothesis 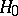 :
:  against the alternative
against the alternative 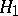 :
: 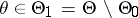 . Suppose that in order to test
. Suppose that in order to test 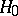 against
against 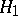 , a non-randomized similar test of level
, a non-randomized similar test of level 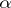 (
(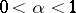 ) has been constructed, with critical function
) has been constructed, with critical function 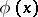 ,
, 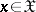 . As this test is non-randomized,
. As this test is non-randomized,
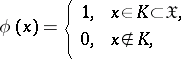 | (1) |
where 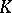 is a certain set in
is a certain set in 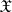 , called the critical set for the test (according to this test, the hypothesis
, called the critical set for the test (according to this test, the hypothesis 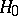 is rejected in favour of
is rejected in favour of 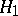 if the event
if the event 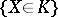 is observed in an experiment). Also, the constructed test is a similar test, which means that
is observed in an experiment). Also, the constructed test is a similar test, which means that
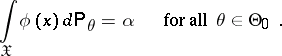 | (2) |
It follows from (1) and (2) that the critical region 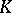 of a non-randomized similar test has the property:
of a non-randomized similar test has the property:
 |
Accordingly, J. Neyman and E.S. Pearson emphasized the latter feature of the critical set of a non-randomized similar test and called 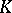 a "region similar to the sample space"
a "region similar to the sample space" 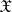 , in the sense that the two probabilities
, in the sense that the two probabilities 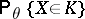 and
and 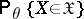 are independent of
are independent of  .
.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | J. Neyman, E.S. Pearson, "On the problem of the most efficient tests of statistical hypotheses" Philos. Trans. Roy. Soc. London Ser. A , 231 (1933) pp. 289–337 |
| [4] | E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation I" Sankhyā , 10 (1950) pp. 305–340 |
| [5] | E.L. Lehmann, H. Scheffé, "Completeness, similar regions, and unbiased estimation II" Sankhyā , 15 (1955) pp. 219–236 |
Similarity region. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Similarity_region&oldid=48701