Sign test
A non-parametric test for a hypothesis 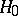 , according to which a random variable
, according to which a random variable 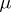 has a binomial distribution with parameters
has a binomial distribution with parameters 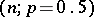 . If the hypothesis
. If the hypothesis 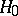 is true, then
is true, then
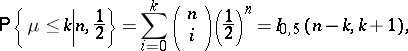 |
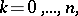 |
where
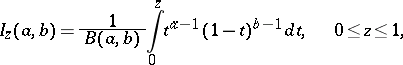 |
and 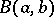 is the beta-function. According to the sign test with significance level
is the beta-function. According to the sign test with significance level 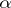 ,
, 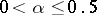 , the hypothesis
, the hypothesis 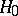 is rejected if
is rejected if
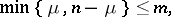 |
where 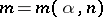 , the critical value of the test, is the integer solution of the inequalities
, the critical value of the test, is the integer solution of the inequalities
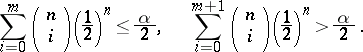 |
The sign test can be used to test a hypothesis 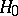 according to which the unknown continuous distribution of independent identically-distributed random variables
according to which the unknown continuous distribution of independent identically-distributed random variables 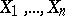 is symmetric about zero, i.e. for any real
is symmetric about zero, i.e. for any real  ,
,
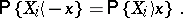 |
In this case the sign test is based on the statistic
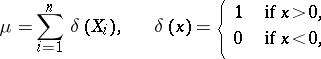 |
which is governed by a binomial law with parameters 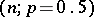 if the hypothesis
if the hypothesis 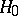 is true.
is true.
Similarly, the sign test is used to test a hypothesis 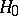 according to which the median of an unknown continuous distribution to which independent random variables
according to which the median of an unknown continuous distribution to which independent random variables 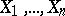 are subject is
are subject is 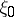 ; to this end one simply replaces the given random variables by
; to this end one simply replaces the given random variables by 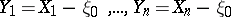 .
.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [3] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [4] | N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian) |
Sign test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sign_test&oldid=48694