User:Maximilian Janisch/latexlist
This is a list of automatically classified LaTeX files. You can manually edit this list, your changes will currently not be considered and only overwritten though.
List
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $\pi$
(confidence 0.45)
: $\pi$
(confidence 0.45)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
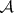 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
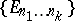 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
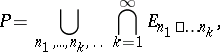 : $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } } \square \ldots x _ { k }$
(confidence 0.10)
: $P = \cup _ { n _ { 1 } , \ldots , n _ { k } , \ldots } \cap _ { k = 1 } ^ { \infty } E _ { x _ { 1 } } \square \ldots x _ { k }$
(confidence 0.10)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
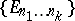 : $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
: $\{ E _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.52)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
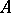 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
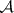 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $\{ A _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ A _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
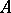 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
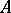 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
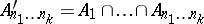 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
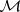 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
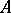 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
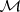 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
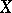 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
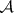 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
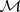 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
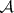 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $\{ A _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
: $\{ A _ { n _ { 1 } \ldots n _ { k } } \}$
(confidence 0.31)
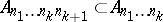 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
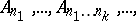 : $A _ { n _ { 1 } } , \ldots , A _ { n _ { 1 } } \ldots n _ { k } , \dots$
(confidence 0.12)
: $A _ { n _ { 1 } } , \ldots , A _ { n _ { 1 } } \ldots n _ { k } , \dots$
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
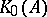 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
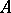 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
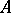 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
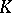 : $4$
(confidence 0.72)
: $4$
(confidence 0.72)
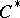 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
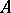 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
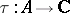 : $\tau : A \rightarrow 1$
(confidence 0.44)
: $\tau : A \rightarrow 1$
(confidence 0.44)
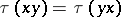 : $\tau ( x y ) = \tau ( y x )$
(confidence 0.66)
: $\tau ( x y ) = \tau ( y x )$
(confidence 0.66)
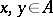 : $x , y \in A$
(confidence 0.96)
: $x , y \in A$
(confidence 0.96)
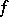 : $t$
(confidence 0.51)
: $t$
(confidence 0.51)
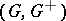 : $( G , G ^ { + } )$
(confidence 1.00)
: $( G , G ^ { + } )$
(confidence 1.00)
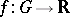 : $f : G \rightarrow R$
(confidence 0.84)
: $f : G \rightarrow R$
(confidence 0.84)
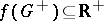 : $f ( G ^ { + } ) \subseteq R ^ { + }$
(confidence 0.97)
: $f ( G ^ { + } ) \subseteq R ^ { + }$
(confidence 0.97)
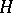 : $e$
(confidence 0.31)
: $e$
(confidence 0.31)
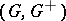 : $( G , G ^ { + } )$
(confidence 1.00)
: $( G , G ^ { + } )$
(confidence 1.00)
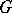 : $x$
(confidence 0.41)
: $x$
(confidence 0.41)
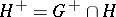 : $H ^ { + } = G ^ { + } \cap H$
(confidence 0.93)
: $H ^ { + } = G ^ { + } \cap H$
(confidence 0.93)
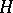 : $e$
(confidence 0.31)
: $e$
(confidence 0.31)
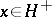 : $x \in H ^ { + }$
(confidence 0.29)
: $x \in H ^ { + }$
(confidence 0.29)
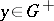 : $y \in G$
(confidence 0.68)
: $y \in G$
(confidence 0.68)
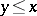 : $y \leq x$
(confidence 1.00)
: $y \leq x$
(confidence 1.00)
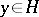 : $y \in H$
(confidence 0.79)
: $y \in H$
(confidence 0.79)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
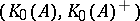 : $( K _ { 0 } ( A ) , K _ { 0 } ( A ) ^ { + } )$
(confidence 0.97)
: $( K _ { 0 } ( A ) , K _ { 0 } ( A ) ^ { + } )$
(confidence 0.97)
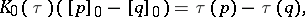 : $K _ { 0 } ( \tau ) ( [ p ] _ { 0 } - [ q ] _ { 0 } ) = \tau ( p ) - \tau ( q$
(confidence 0.68)
: $K _ { 0 } ( \tau ) ( [ p ] _ { 0 } - [ q ] _ { 0 } ) = \tau ( p ) - \tau ( q$
(confidence 0.68)
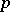 : $m$
(confidence 0.16)
: $m$
(confidence 0.16)
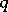 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
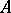 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
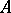 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
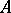 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
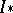 : $1 \times$
(confidence 0.27)
: $1 \times$
(confidence 0.27)
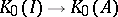 : $K _ { 0 } ( I ) \rightarrow K _ { 0 } ( A )$
(confidence 0.74)
: $K _ { 0 } ( I ) \rightarrow K _ { 0 } ( A )$
(confidence 0.74)
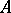 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
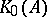 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
 : $\tau \mapsto K _ { 0 } ( \tau )$
(confidence 0.92)
: $\tau \mapsto K _ { 0 } ( \tau )$
(confidence 0.92)
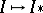 : $I \mapsto I$
(confidence 0.14)
: $I \mapsto I$
(confidence 0.14)
 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
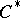 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
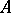 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
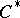 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
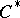 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
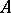 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
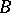 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
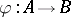 : $\varphi : A \rightarrow B$
(confidence 0.94)
: $\varphi : A \rightarrow B$
(confidence 0.94)
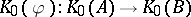 : $K _ { 0 } ( \varphi ) : K _ { 0 } ( A ) \rightarrow K _ { 0 } ( B )$
(confidence 0.77)
: $K _ { 0 } ( \varphi ) : K _ { 0 } ( A ) \rightarrow K _ { 0 } ( B )$
(confidence 0.77)
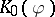 : $06$
(confidence 0.34)
: $06$
(confidence 0.34)
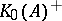 : $K _ { 0 } ( A ) ^ { + }$
(confidence 0.92)
: $K _ { 0 } ( A ) ^ { + }$
(confidence 0.92)
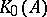 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
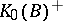 : $K _ { 0 } ( B ) ^ { + }$
(confidence 0.82)
: $K _ { 0 } ( B ) ^ { + }$
(confidence 0.82)
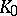 : $x ^ { 2 }$
(confidence 0.13)
: $x ^ { 2 }$
(confidence 0.13)
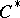 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
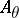 : $A$
(confidence 0.93)
: $A$
(confidence 0.93)
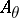 : $A$
(confidence 0.93)
: $A$
(confidence 0.93)
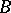 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
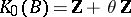 : $K _ { 0 } ( B ) = Z + \vec { \theta } Z$
(confidence 0.18)
: $K _ { 0 } ( B ) = Z + \vec { \theta } Z$
(confidence 0.18)
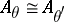 : $A _ { \theta } \cong A _ { \theta }$
(confidence 0.94)
: $A _ { \theta } \cong A _ { \theta }$
(confidence 0.94)
 : $\theta = \theta$
(confidence 1.00)
: $\theta = \theta$
(confidence 1.00)
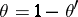 : $\theta = 1 - \theta$
(confidence 0.74)
: $\theta = 1 - \theta$
(confidence 0.74)
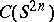 : $C ( S ^ { 2 n }$
(confidence 0.84)
: $C ( S ^ { 2 n }$
(confidence 0.84)
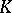 : $4$
(confidence 0.72)
: $4$
(confidence 0.72)
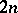 : $3$
(confidence 0.43)
: $3$
(confidence 0.43)
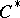 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
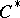 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
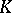 : $4$
(confidence 0.72)
: $4$
(confidence 0.72)
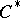 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
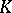 : $4$
(confidence 0.72)
: $4$
(confidence 0.72)
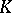 : $4$
(confidence 0.72)
: $4$
(confidence 0.72)
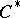 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
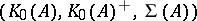 : $( K _ { 0 } ( A ) , K _ { 0 } ( A ) ^ { + } , \Sigma ( A ) )$
(confidence 0.94)
: $( K _ { 0 } ( A ) , K _ { 0 } ( A ) ^ { + } , \Sigma ( A ) )$
(confidence 0.94)
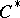 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
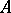 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
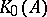 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
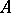 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
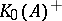 : $K _ { 0 } ( A ) ^ { + }$
(confidence 0.92)
: $K _ { 0 } ( A ) ^ { + }$
(confidence 0.92)
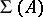 : $\Sigma ( A$
(confidence 0.79)
: $\Sigma ( A$
(confidence 0.79)
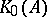 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
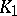 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
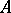 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
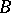 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $7$
(confidence 0.87)
: $7$
(confidence 0.87)
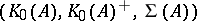 : $( K _ { 0 } ( A ) , K _ { 0 } ( A ) ^ { + } , \Sigma ( A ) )$
(confidence 0.95)
: $( K _ { 0 } ( A ) , K _ { 0 } ( A ) ^ { + } , \Sigma ( A ) )$
(confidence 0.95)
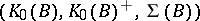 : $( K _ { 0 } ( B ) , K _ { 0 } ( B ) ^ { + } , \Sigma ( B ) )$
(confidence 0.96)
: $( K _ { 0 } ( B ) , K _ { 0 } ( B ) ^ { + } , \Sigma ( B ) )$
(confidence 0.96)
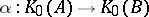 : $\alpha : K _ { 0 } ( A ) \rightarrow K _ { 0 } ( B )$
(confidence 0.88)
: $\alpha : K _ { 0 } ( A ) \rightarrow K _ { 0 } ( B )$
(confidence 0.88)
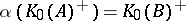 : $\alpha ( K _ { 0 } ( A ) ^ { + } ) = K _ { 0 } ( B ) ^ { + }$
(confidence 0.80)
: $\alpha ( K _ { 0 } ( A ) ^ { + } ) = K _ { 0 } ( B ) ^ { + }$
(confidence 0.80)
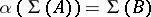 : $\alpha ( \Sigma ( A ) ) = \Sigma ( B )$
(confidence 0.81)
: $\alpha ( \Sigma ( A ) ) = \Sigma ( B )$
(confidence 0.81)
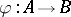 : $\varphi : A \rightarrow B$
(confidence 0.94)
: $\varphi : A \rightarrow B$
(confidence 0.94)
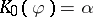 : $K _ { 0 } ( \varphi ) = a$
(confidence 0.81)
: $K _ { 0 } ( \varphi ) = a$
(confidence 0.81)
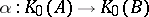 : $\alpha : K _ { 0 } ( A ) \rightarrow K _ { 0 } ( B )$
(confidence 0.88)
: $\alpha : K _ { 0 } ( A ) \rightarrow K _ { 0 } ( B )$
(confidence 0.88)
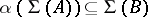 : $\alpha ( \Sigma ( A ) ) \subseteq \Sigma ( B )$
(confidence 0.74)
: $\alpha ( \Sigma ( A ) ) \subseteq \Sigma ( B )$
(confidence 0.74)
 : $7$
(confidence 0.87)
: $7$
(confidence 0.87)
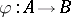 : $\varphi : A \rightarrow B$
(confidence 0.94)
: $\varphi : A \rightarrow B$
(confidence 0.94)
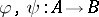 : $\varphi , \psi : A \rightarrow B$
(confidence 0.97)
: $\varphi , \psi : A \rightarrow B$
(confidence 0.97)
 : $7$
(confidence 0.87)
: $7$
(confidence 0.87)
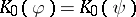 : $K _ { 0 } ( \varphi ) = K _ { 0 } ( \psi )$
(confidence 0.92)
: $K _ { 0 } ( \varphi ) = K _ { 0 } ( \psi )$
(confidence 0.92)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
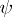 : $- 1$
(confidence 0.08)
: $- 1$
(confidence 0.08)
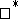 : $7$
(confidence 0.87)
: $7$
(confidence 0.87)
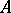 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
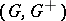 : $( G , G ^ { + } )$
(confidence 1.00)
: $( G , G ^ { + } )$
(confidence 1.00)
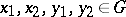 : $x _ { 1 } , x _ { 2 } , y _ { 1 } , y _ { 2 } \in G$
(confidence 0.78)
: $x _ { 1 } , x _ { 2 } , y _ { 1 } , y _ { 2 } \in G$
(confidence 0.78)
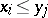 : $x _ { i } \leq y _ { 1 }$
(confidence 0.29)
: $x _ { i } \leq y _ { 1 }$
(confidence 0.29)
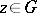 : $z \in r$
(confidence 0.38)
: $z \in r$
(confidence 0.38)
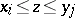 : $x _ { i } \leq z \leq y _ { j }$
(confidence 0.19)
: $x _ { i } \leq z \leq y _ { j }$
(confidence 0.19)
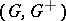 : $( G , G ^ { + } )$
(confidence 1.00)
: $( G , G ^ { + } )$
(confidence 1.00)
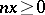 : $3$
(confidence 0.39)
: $3$
(confidence 0.39)
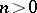 : $n > 1$
(confidence 0.81)
: $n > 1$
(confidence 0.81)
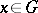 : $x \in r$
(confidence 0.67)
: $x \in r$
(confidence 0.67)
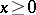 : $x > 0$
(confidence 1.00)
: $x > 0$
(confidence 1.00)
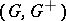 : $( G , G ^ { + } )$
(confidence 1.00)
: $( G , G ^ { + } )$
(confidence 1.00)
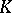 : $4$
(confidence 0.72)
: $4$
(confidence 0.72)
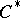 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
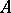 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
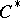 : $C$
(confidence 0.76)
: $C$
(confidence 0.76)
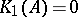 : $K _ { 1 } ( A ) = 0$
(confidence 0.98)
: $K _ { 1 } ( A ) = 0$
(confidence 0.98)
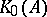 : $_ { 0 } ( A$
(confidence 0.08)
: $_ { 0 } ( A$
(confidence 0.08)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
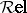 : $\sqrt { 2 } e$
(confidence 0.37)
: $\sqrt { 2 } e$
(confidence 0.37)
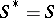 : $S ^ { * } = S$
(confidence 0.90)
: $S ^ { * } = S$
(confidence 0.90)
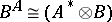 : $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
: $B ^ { A } \cong ( A ^ { * } \otimes B )$
(confidence 1.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.26)
: $( - ) ^ { * } : C ^ { 0 p } \rightarrow C$
(confidence 0.26)
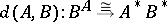 : $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.75)
: $d ( A , B ) : B ^ { A } \cong A ^ { * } B ^ { * }$
(confidence 0.75)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
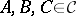 : $A , B , C \in C$
(confidence 0.99)
: $A , B , C \in C$
(confidence 0.99)
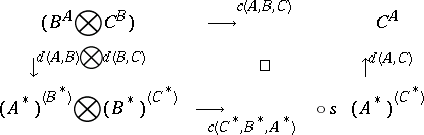 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.40)
: $s = s ( ( A ^ { * } ) ^ { ( B ^ { * } ) } , ( B ^ { * } ) ^ { ( C ^ { * } ) } )$
(confidence 0.40)
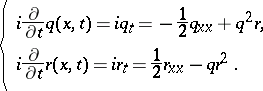 : $\left. \begin{array} { l } { i \frac { \partial } { \partial t } q ( x , t ) = i q _ { t } = - \frac { 1 } { 2 } q x _ { x } + q ^ { 2 } r } \\ { i \frac { \partial } { \partial t } r ( x , t ) = i r _ { t } = \frac { 1 } { 2 } r _ { X x } - q r ^ { 2 } } \end{array} \right.$
(confidence 0.37)
: $\left. \begin{array} { l } { i \frac { \partial } { \partial t } q ( x , t ) = i q _ { t } = - \frac { 1 } { 2 } q x _ { x } + q ^ { 2 } r } \\ { i \frac { \partial } { \partial t } r ( x , t ) = i r _ { t } = \frac { 1 } { 2 } r _ { X x } - q r ^ { 2 } } \end{array} \right.$
(confidence 0.37)
 : $t = ( t _ { n }$
(confidence 0.41)
: $t = ( t _ { n }$
(confidence 0.41)
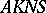 : $4 K N$
(confidence 0.52)
: $4 K N$
(confidence 0.52)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
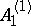 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
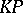 : $K P$
(confidence 0.56)
: $K P$
(confidence 0.56)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
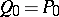 : $Q _ { 0 } = P$
(confidence 0.62)
: $Q _ { 0 } = P$
(confidence 0.62)
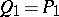 : $Q _ { 1 } = P _ { 1 }$
(confidence 0.67)
: $Q _ { 1 } = P _ { 1 }$
(confidence 0.67)
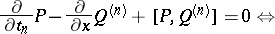 : $\frac { \partial } { \partial t _ { n } } P - \frac { \partial } { \partial x } Q ^ { ( n ) } + [ P , Q ^ { ( n ) } ] = 0 \Leftrightarrow$
(confidence 0.66)
: $\frac { \partial } { \partial t _ { n } } P - \frac { \partial } { \partial x } Q ^ { ( n ) } + [ P , Q ^ { ( n ) } ] = 0 \Leftrightarrow$
(confidence 0.66)
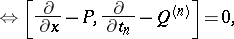 : $\Leftrightarrow [ \frac { \partial } { \partial x } - P , \frac { \partial } { \partial t _ { n } } - Q ^ { ( n ) } ] = 0$
(confidence 0.64)
: $\Leftrightarrow [ \frac { \partial } { \partial x } - P , \frac { \partial } { \partial t _ { n } } - Q ^ { ( n ) } ] = 0$
(confidence 0.64)
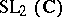 : $L _ { 2 } CC$
(confidence 0.07)
: $L _ { 2 } CC$
(confidence 0.07)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
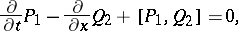 : $\frac { \partial } { \partial t } P _ { 1 } - \frac { \partial } { \partial x } Q _ { 2 } + [ P _ { 1 } , Q _ { 2 } ] = 0$
(confidence 0.98)
: $\frac { \partial } { \partial t } P _ { 1 } - \frac { \partial } { \partial x } Q _ { 2 } + [ P _ { 1 } , Q _ { 2 } ] = 0$
(confidence 0.98)
 : $5$
(confidence 0.50)
: $5$
(confidence 0.50)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
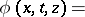 : $( x , t , z ) =$
(confidence 0.97)
: $( x , t , z ) =$
(confidence 0.97)
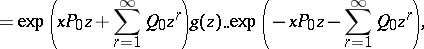 : $= \operatorname { exp } ( x P _ { 0 } z + \sum _ { r = 1 } ^ { \infty } Q _ { 0 } z ^ { r } ) g ( z ) . . \operatorname { exp } ( - x P _ { 0 } z - \sum _ { r = 1 } ^ { \infty } Q _ { 0 } z ^ { r } )$
(confidence 0.62)
: $= \operatorname { exp } ( x P _ { 0 } z + \sum _ { r = 1 } ^ { \infty } Q _ { 0 } z ^ { r } ) g ( z ) . . \operatorname { exp } ( - x P _ { 0 } z - \sum _ { r = 1 } ^ { \infty } Q _ { 0 } z ^ { r } )$
(confidence 0.62)
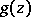 : $g ( z$
(confidence 0.96)
: $g ( z$
(confidence 0.96)
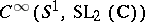 : $C ^ { \infty } ( S ^ { 1 } , SL _ { 2 } ( C ) )$
(confidence 0.76)
: $C ^ { \infty } ( S ^ { 1 } , SL _ { 2 } ( C ) )$
(confidence 0.76)
 : $m$
(confidence 0.08)
: $m$
(confidence 0.08)
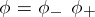 : $\phi = \phi _ { - } \phi _ { + }$
(confidence 0.82)
: $\phi = \phi _ { - } \phi _ { + }$
(confidence 0.82)
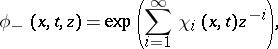 : $\phi _ { - } ( x , t , z ) = \operatorname { exp } ( \sum _ { i = 1 } ^ { \infty } \chi _ { i } ( x , t ) z ^ { - i } )$
(confidence 0.87)
: $\phi _ { - } ( x , t , z ) = \operatorname { exp } ( \sum _ { i = 1 } ^ { \infty } \chi _ { i } ( x , t ) z ^ { - i } )$
(confidence 0.87)
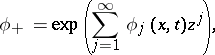 : $\phi _ { + } = \operatorname { exp } ( \sum _ { j = 1 } ^ { \infty } \phi j ( x , t ) z ^ { j } )$
(confidence 0.60)
: $\phi _ { + } = \operatorname { exp } ( \sum _ { j = 1 } ^ { \infty } \phi j ( x , t ) z ^ { j } )$
(confidence 0.60)
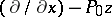 : $( \partial / \partial x ) - P _ { 0 } z$
(confidence 0.83)
: $( \partial / \partial x ) - P _ { 0 } z$
(confidence 0.83)
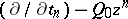 : $( \partial / \partial t _ { n } ) - Q _ { 0 } z ^ { \prime }$
(confidence 0.30)
: $( \partial / \partial t _ { n } ) - Q _ { 0 } z ^ { \prime }$
(confidence 0.30)
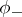 : $( 3 )$
(confidence 0.42)
: $( 3 )$
(confidence 0.42)
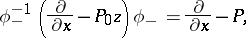 : $\phi _ { - } ^ { - 1 } ( \frac { \partial } { \partial x } - P b z ) \phi _ { - } = \frac { \partial } { \partial x } - P$
(confidence 0.43)
: $\phi _ { - } ^ { - 1 } ( \frac { \partial } { \partial x } - P b z ) \phi _ { - } = \frac { \partial } { \partial x } - P$
(confidence 0.43)
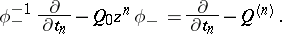 : $\phi _ { - } ^ { - 1 } \frac { \partial } { \partial t _ { n } } - Q _ { 0 } z ^ { n } \phi _ { - } = \frac { \partial } { \partial t _ { n } } - Q ^ { ( n ) }$
(confidence 0.50)
: $\phi _ { - } ^ { - 1 } \frac { \partial } { \partial t _ { n } } - Q _ { 0 } z ^ { n } \phi _ { - } = \frac { \partial } { \partial t _ { n } } - Q ^ { ( n ) }$
(confidence 0.50)
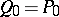 : $Q _ { 0 } = P$
(confidence 0.62)
: $Q _ { 0 } = P$
(confidence 0.62)
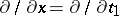 : $\partial x = \partial / \partial t$
(confidence 0.83)
: $\partial x = \partial / \partial t$
(confidence 0.83)
 : $L _ { 2 } CC$
(confidence 0.07)
: $L _ { 2 } CC$
(confidence 0.07)
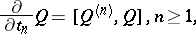 : $\frac { \partial } { \partial t _ { t } } Q = [ Q ^ { ( n ) } , g ] , n \geq 1$
(confidence 0.47)
: $\frac { \partial } { \partial t _ { t } } Q = [ Q ^ { ( n ) } , g ] , n \geq 1$
(confidence 0.47)
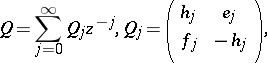 : $Q = \sum _ { j = 0 } ^ { \infty } Q _ { j } z ^ { - j } , Q _ { j } = \left( \begin{array} { c c } { h _ { j } } & { e _ { j } } \\ { f _ { j } } & { - h _ { j } } \end{array} \right)$
(confidence 0.58)
: $Q = \sum _ { j = 0 } ^ { \infty } Q _ { j } z ^ { - j } , Q _ { j } = \left( \begin{array} { c c } { h _ { j } } & { e _ { j } } \\ { f _ { j } } & { - h _ { j } } \end{array} \right)$
(confidence 0.58)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
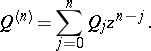 : $Q ^ { ( n ) } = \sum _ { j = 0 } ^ { N } Q _ { j } z ^ { n - j }$
(confidence 0.25)
: $Q ^ { ( n ) } = \sum _ { j = 0 } ^ { N } Q _ { j } z ^ { n - j }$
(confidence 0.25)
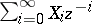 : $\sum _ { i = 0 } ^ { \infty } X _ { i } z ^ { - t }$
(confidence 0.92)
: $\sum _ { i = 0 } ^ { \infty } X _ { i } z ^ { - t }$
(confidence 0.92)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
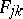 : $F _ { i , j }$
(confidence 0.10)
: $F _ { i , j }$
(confidence 0.10)
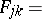 : $F _ { j k } =$
(confidence 0.80)
: $F _ { j k } =$
(confidence 0.80)
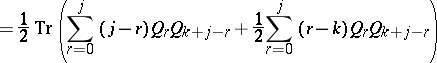 : $= \frac { 1 } { 2 } \operatorname { Tr } ( \sum _ { r = 0 } ^ { j } ( j - r ) Q _ { r } Q _ { k + j - \gamma } + \frac { 1 } { 2 } \sum _ { r = 0 } ^ { j } ( r - k ) Q _ { r } Q _ { k + j - r }$
(confidence 0.20)
: $= \frac { 1 } { 2 } \operatorname { Tr } ( \sum _ { r = 0 } ^ { j } ( j - r ) Q _ { r } Q _ { k + j - \gamma } + \frac { 1 } { 2 } \sum _ { r = 0 } ^ { j } ( r - k ) Q _ { r } Q _ { k + j - r }$
(confidence 0.20)
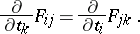 : $\frac { \partial } { \partial t _ { k } } F _ { i j } = \frac { \partial } { \partial t _ { i } } F _ { j k }$
(confidence 0.91)
: $\frac { \partial } { \partial t _ { k } } F _ { i j } = \frac { \partial } { \partial t _ { i } } F _ { j k }$
(confidence 0.91)
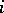 : $ $
(confidence 0.11)
: $ $
(confidence 0.11)
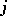 : $7$
(confidence 0.49)
: $7$
(confidence 0.49)
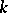 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
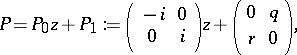 : $P = P _ { 0 } z + P _ { 1 } : = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) z + \left( \begin{array} { l l } { 0 } & { q } \\ { r } & { 0 } \end{array} \right)$
(confidence 0.46)
: $P = P _ { 0 } z + P _ { 1 } : = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) z + \left( \begin{array} { l l } { 0 } & { q } \\ { r } & { 0 } \end{array} \right)$
(confidence 0.46)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
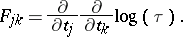 : $F _ { j k } = \frac { \partial } { \partial t _ { j } } \frac { \partial } { \partial t _ { k } } \operatorname { log } ( \tau )$
(confidence 0.99)
: $F _ { j k } = \frac { \partial } { \partial t _ { j } } \frac { \partial } { \partial t _ { k } } \operatorname { log } ( \tau )$
(confidence 0.99)
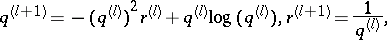 : $q ^ { ( l + 1 ) } = - ( q ^ { ( l ) } ) ^ { 2 } r ^ { ( l ) } + q ^ { ( l ) } \operatorname { log } ( q ^ { ( l ) } ) , r ^ { ( l + 1 ) } = \frac { 1 } { q ^ { ( l ) } }$
(confidence 0.52)
: $q ^ { ( l + 1 ) } = - ( q ^ { ( l ) } ) ^ { 2 } r ^ { ( l ) } + q ^ { ( l ) } \operatorname { log } ( q ^ { ( l ) } ) , r ^ { ( l + 1 ) } = \frac { 1 } { q ^ { ( l ) } }$
(confidence 0.52)
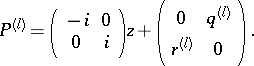 : $P ^ { ( l ) } = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) z + \left( \begin{array} { c c } { 0 } & { q ^ { ( l ) } } \\ { r ^ { ( l ) } } & { 0 } \end{array} \right)$
(confidence 0.62)
: $P ^ { ( l ) } = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) z + \left( \begin{array} { c c } { 0 } & { q ^ { ( l ) } } \\ { r ^ { ( l ) } } & { 0 } \end{array} \right)$
(confidence 0.62)
 : $x$
(confidence 0.20)
: $x$
(confidence 0.20)
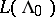 : $L ( \Lambda _ { 0 }$
(confidence 0.80)
: $L ( \Lambda _ { 0 }$
(confidence 0.80)
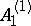 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
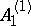 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
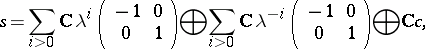 : $= \sum _ { i > 0 } C \lambda ^ { i } \left( \begin{array} { c c } { - 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) \oplus \sum _ { i > 0 } C \lambda ^ { - i } \left( \begin{array} { c c } { - 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) \oplus C _ { c }$
(confidence 0.14)
: $= \sum _ { i > 0 } C \lambda ^ { i } \left( \begin{array} { c c } { - 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) \oplus \sum _ { i > 0 } C \lambda ^ { - i } \left( \begin{array} { c c } { - 1 } & { 0 } \\ { 0 } & { 1 } \end{array} \right) \oplus C _ { c }$
(confidence 0.14)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
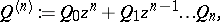 : $Q ^ { ( n ) } : = Q _ { 0 } z ^ { n } + Q _ { 1 } z ^ { n - 1 } \ldots Q _ { x }$
(confidence 0.54)
: $Q ^ { ( n ) } : = Q _ { 0 } z ^ { n } + Q _ { 1 } z ^ { n - 1 } \ldots Q _ { x }$
(confidence 0.54)
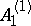 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
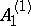 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
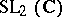 : $L _ { 2 } CC$
(confidence 0.07)
: $L _ { 2 } CC$
(confidence 0.07)
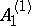 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
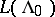 : $L ( \Lambda _ { 0 }$
(confidence 0.80)
: $L ( \Lambda _ { 0 }$
(confidence 0.80)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
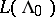 : $L ( \Lambda _ { 0 }$
(confidence 0.80)
: $L ( \Lambda _ { 0 }$
(confidence 0.80)
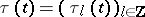 : $\tau ( t ) = ( \tau _ { l } ( t ) ) _ { l \in T }$
(confidence 0.27)
: $\tau ( t ) = ( \tau _ { l } ( t ) ) _ { l \in T }$
(confidence 0.27)
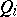 : $x ^ { 2 }$
(confidence 0.30)
: $x ^ { 2 }$
(confidence 0.30)
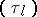 : $T _ { l }$
(confidence 0.54)
: $T _ { l }$
(confidence 0.54)
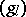 : $( g )$
(confidence 0.72)
: $( g )$
(confidence 0.72)
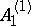 : $A _ { 1 }$
(confidence 0.38)
: $A _ { 1 }$
(confidence 0.38)
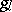 : $4$
(confidence 0.29)
: $4$
(confidence 0.29)
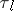 : $1$
(confidence 0.70)
: $1$
(confidence 0.70)
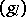 : $( g )$
(confidence 0.72)
: $( g )$
(confidence 0.72)
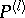 : $P ( 0$
(confidence 0.35)
: $P ( 0$
(confidence 0.35)
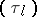 : $T _ { l }$
(confidence 0.54)
: $T _ { l }$
(confidence 0.54)
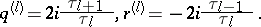 : $q ^ { ( l ) } = 2 i \frac { T l + 1 } { \tau l } , r ^ { ( l ) } = - 2 i \frac { \tau l - 1 } { \tau l }$
(confidence 0.13)
: $q ^ { ( l ) } = 2 i \frac { T l + 1 } { \tau l } , r ^ { ( l ) } = - 2 i \frac { \tau l - 1 } { \tau l }$
(confidence 0.13)
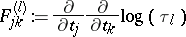 : $F _ { j k } ^ { ( l ) } : = \frac { \partial } { \partial t _ { j } } \frac { \partial } { \partial t _ { k } } \operatorname { log } ( \tau _ { l } )$
(confidence 0.89)
: $F _ { j k } ^ { ( l ) } : = \frac { \partial } { \partial t _ { j } } \frac { \partial } { \partial t _ { k } } \operatorname { log } ( \tau _ { l } )$
(confidence 0.89)
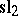 : $512$
(confidence 0.21)
: $512$
(confidence 0.21)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
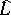 : $T$
(confidence 0.22)
: $T$
(confidence 0.22)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $T$
(confidence 0.22)
: $T$
(confidence 0.22)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $L : = P _ { 0 } \frac { d } { d x } + P _ { 1 } = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) \frac { d } { d x } + \left( \begin{array} { l l } { 0 } & { q } \\ { r } & { 0 } \end{array} \right)$
(confidence 0.90)
: $L : = P _ { 0 } \frac { d } { d x } + P _ { 1 } = \left( \begin{array} { c c } { - i } & { 0 } \\ { 0 } & { i } \end{array} \right) \frac { d } { d x } + \left( \begin{array} { l l } { 0 } & { q } \\ { r } & { 0 } \end{array} \right)$
(confidence 0.90)
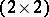 : $2 \times 2$
(confidence 1.00)
: $2 \times 2$
(confidence 1.00)
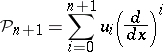 : $P _ { n + 1 } = \sum _ { i = 0 } ^ { n + 1 } u _ { i } ( \frac { d } { d x } ) ^ { t }$
(confidence 0.30)
: $P _ { n + 1 } = \sum _ { i = 0 } ^ { n + 1 } u _ { i } ( \frac { d } { d x } ) ^ { t }$
(confidence 0.30)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
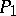 : $f ^ { 2 }$
(confidence 0.11)
: $f ^ { 2 }$
(confidence 0.11)
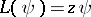 : $L ( \psi ) = z \psi$
(confidence 0.94)
: $L ( \psi ) = z \psi$
(confidence 0.94)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
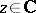 : $7$
(confidence 1.00)
: $7$
(confidence 1.00)
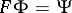 : $F \Phi = \Psi$
(confidence 0.48)
: $F \Phi = \Psi$
(confidence 0.48)
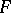 : $r$
(confidence 0.12)
: $r$
(confidence 0.12)
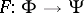 : $\Phi \rightarrow \Psi$
(confidence 0.78)
: $\Phi \rightarrow \Psi$
(confidence 0.78)
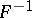 : $F ^ { \prime }$
(confidence 0.11)
: $F ^ { \prime }$
(confidence 0.11)
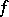 : $t$
(confidence 0.51)
: $t$
(confidence 0.51)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
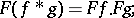 : $F ( f ^ { * } g ) = F f . F g$
(confidence 0.68)
: $F ( f ^ { * } g ) = F f . F g$
(confidence 0.68)
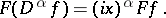 : $F ( D ^ { \alpha } f ) = ( i x ) ^ { \alpha } F f$
(confidence 0.77)
: $F ( D ^ { \alpha } f ) = ( i x ) ^ { \alpha } F f$
(confidence 0.77)
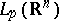 : $L _ { p } ( R ^ { n } )$
(confidence 0.88)
: $L _ { p } ( R ^ { n } )$
(confidence 0.88)
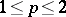 : $\leq p \leq 2$
(confidence 0.28)
: $\leq p \leq 2$
(confidence 0.28)
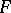 : $r$
(confidence 0.12)
: $r$
(confidence 0.12)
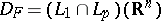 : $D _ { F } = ( L _ { 1 } \cap L _ { p } ) ( R ^ { n } )$
(confidence 0.26)
: $D _ { F } = ( L _ { 1 } \cap L _ { p } ) ( R ^ { n } )$
(confidence 0.26)
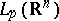 : $L _ { p } ( R ^ { n } )$
(confidence 0.88)
: $L _ { p } ( R ^ { n } )$
(confidence 0.88)
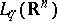 : $L _ { \varphi } ( R ^ { n } )$
(confidence 0.23)
: $L _ { \varphi } ( R ^ { n } )$
(confidence 0.23)
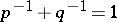 : $p ^ { - 1 } + q ^ { - 1 } = 1$
(confidence 1.00)
: $p ^ { - 1 } + q ^ { - 1 } = 1$
(confidence 1.00)
 : $r$
(confidence 0.12)
: $r$
(confidence 0.12)
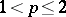 : $1 < p \leq 2$
(confidence 1.00)
: $1 < p \leq 2$
(confidence 1.00)
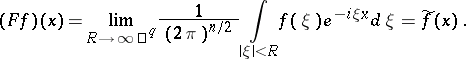 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
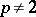 : $p \neq 2$
(confidence 1.00)
: $p \neq 2$
(confidence 1.00)
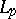 : $x$
(confidence 0.13)
: $x$
(confidence 0.13)
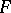 : $r$
(confidence 0.12)
: $r$
(confidence 0.12)
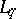 : $x$
(confidence 0.33)
: $x$
(confidence 0.33)
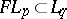 : $F L _ { p } \subset l _ { q }$
(confidence 0.43)
: $F L _ { p } \subset l _ { q }$
(confidence 0.43)
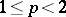 : $\leq p < 2$
(confidence 0.31)
: $\leq p < 2$
(confidence 0.31)
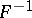 : $F ^ { \prime }$
(confidence 0.11)
: $F ^ { \prime }$
(confidence 0.11)
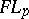 : $F L y$
(confidence 0.94)
: $F L y$
(confidence 0.94)
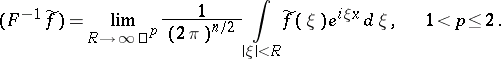 : $( F ^ { - 1 } \tilde { f } ) = \operatorname { lim } _ { R \rightarrow \infty } \frac { 1 } { ( 2 \pi ) ^ { n / 2 } } \int _ { | \xi | < R } \tilde { f } ( \xi ) e ^ { i \xi x } d \xi , \quad 1 < p \leq 2$
(confidence 0.17)
: $( F ^ { - 1 } \tilde { f } ) = \operatorname { lim } _ { R \rightarrow \infty } \frac { 1 } { ( 2 \pi ) ^ { n / 2 } } \int _ { | \xi | < R } \tilde { f } ( \xi ) e ^ { i \xi x } d \xi , \quad 1 < p \leq 2$
(confidence 0.17)
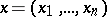 : $x = ( x _ { 1 } , \ldots , x _ { n } )$
(confidence 0.08)
: $x = ( x _ { 1 } , \ldots , x _ { n } )$
(confidence 0.08)
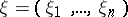 : $\xi = ( \xi _ { 1 } , \ldots , \xi _ { n } )$
(confidence 0.53)
: $\xi = ( \xi _ { 1 } , \ldots , \xi _ { n } )$
(confidence 0.53)
 : $x$
(confidence 0.66)
: $x$
(confidence 0.66)
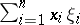 : $\sum _ { i = 1 } ^ { 8 } x _ { i } \xi$
(confidence 0.12)
: $\sum _ { i = 1 } ^ { 8 } x _ { i } \xi$
(confidence 0.12)
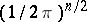 : $( 1 / 2 \pi ) ^ { n / 2 }$
(confidence 1.00)
: $( 1 / 2 \pi ) ^ { n / 2 }$
(confidence 1.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
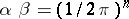 : $\beta = ( 1 / 2 \pi ) ^ { x }$
(confidence 0.91)
: $\beta = ( 1 / 2 \pi ) ^ { x }$
(confidence 0.91)
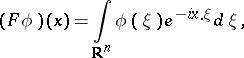 : $( F \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { - i x \cdot \xi } d \xi$
(confidence 0.31)
: $( F \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { - i x \cdot \xi } d \xi$
(confidence 0.31)
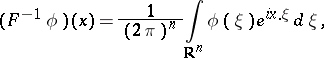 : $( F ^ { - 1 } \phi ) ( x ) = \frac { 1 } { ( 2 \pi ) ^ { n } } \int _ { R ^ { n } } \phi ( \xi ) e ^ { i x . \xi } d \xi$
(confidence 0.50)
: $( F ^ { - 1 } \phi ) ( x ) = \frac { 1 } { ( 2 \pi ) ^ { n } } \int _ { R ^ { n } } \phi ( \xi ) e ^ { i x . \xi } d \xi$
(confidence 0.50)
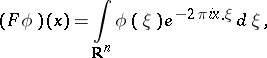 : $( F \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { - 2 \pi i x . \xi } d \xi$
(confidence 0.16)
: $( F \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { - 2 \pi i x . \xi } d \xi$
(confidence 0.16)
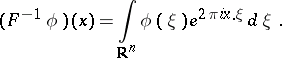 : $( F ^ { - 1 } \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { 2 \pi i x . \xi } d \xi$
(confidence 0.08)
: $( F ^ { - 1 } \phi ) ( x ) = \int _ { R ^ { n } } \phi ( \xi ) e ^ { 2 \pi i x . \xi } d \xi$
(confidence 0.08)
 : $L _ { 2 } ( R ^ { * } )$
(confidence 0.33)
: $L _ { 2 } ( R ^ { * } )$
(confidence 0.33)
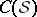 : $C ( S$
(confidence 0.88)
: $C ( S$
(confidence 0.88)
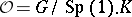 : $O = G / Sp ( 1 ) . K$
(confidence 0.35)
: $O = G / Sp ( 1 ) . K$
(confidence 0.35)
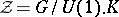 : $Z = G / U ( 1 ) . K$
(confidence 0.85)
: $Z = G / U ( 1 ) . K$
(confidence 0.85)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
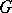 : $x$
(confidence 0.41)
: $x$
(confidence 0.41)
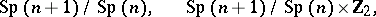 : $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times 2$
(confidence 0.10)
: $\operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) , \quad \operatorname { Sp } ( n + 1 ) / \operatorname { Sp } ( n ) \times 2$
(confidence 0.10)
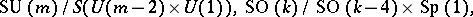 : $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times$
(confidence 0.10)
: $SU ( m ) / S ( U ( m - 2 ) \times U ( 1 ) ) , SO ( k ) / SO ( k - 4 ) \times$
(confidence 0.10)
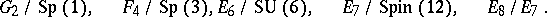 : $\Delta$
(confidence 0.32)
: $\Delta$
(confidence 0.32)
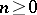 : $n > 0$
(confidence 1.00)
: $n > 0$
(confidence 1.00)
 : $p ( 0$
(confidence 0.93)
: $p ( 0$
(confidence 0.93)
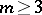 : $m > 3$
(confidence 0.98)
: $m > 3$
(confidence 0.98)
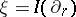 : $\xi = I ( \partial _ { y } )$
(confidence 0.65)
: $\xi = I ( \partial _ { y } )$
(confidence 0.65)
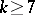 : $x > 7$
(confidence 0.72)
: $x > 7$
(confidence 0.72)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
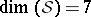 : $( S ) = 7$
(confidence 0.98)
: $( S ) = 7$
(confidence 0.98)
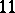 : $I$
(confidence 0.24)
: $I$
(confidence 0.24)
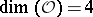 : $( O ) = \mathfrak { L }$
(confidence 0.41)
: $( O ) = \mathfrak { L }$
(confidence 0.41)
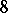 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
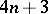 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
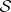 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
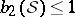 : $( S ) \leq 1$
(confidence 0.54)
: $( S ) \leq 1$
(confidence 0.54)
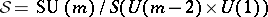 : $S = \operatorname { SU } ( m ) / S ( U ( m - 2 ) \times U ( 1 )$
(confidence 0.36)
: $S = \operatorname { SU } ( m ) / S ( U ( m - 2 ) \times U ( 1 )$
(confidence 0.36)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
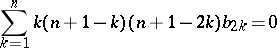 : $\sum ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.74)
: $\sum ^ { n } k ( n + 1 - k ) ( n + 1 - 2 k ) b _ { 2 k } = 0$
(confidence 0.74)
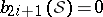 : $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.91)
: $b _ { 2 i + 1 } ( S ) = 0$
(confidence 0.91)
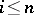 : $i < n$
(confidence 0.92)
: $i < n$
(confidence 0.92)
 : $I$
(confidence 0.24)
: $I$
(confidence 0.24)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
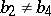 : $b _ { 2 } \neq b$
(confidence 0.48)
: $b _ { 2 } \neq b$
(confidence 0.48)
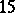 : $1.3$
(confidence 0.59)
: $1.3$
(confidence 0.59)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
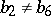 : $b _ { 2 } \neq b _ { 6 }$
(confidence 0.79)
: $b _ { 2 } \neq b _ { 6 }$
(confidence 0.79)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
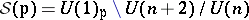 : $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.71)
: $S ( p ) = U ( 1 ) _ { p } \backslash U ( n + 2 ) / U ( n )$
(confidence 0.71)
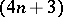 : $( 4 n + 3 )$
(confidence 1.00)
: $( 4 n + 3 )$
(confidence 1.00)
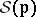 : $S ( D$
(confidence 0.16)
: $S ( D$
(confidence 0.16)
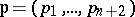 : $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.59)
: $p = ( p _ { 1 } , \dots , p _ { n } + 2 )$
(confidence 0.59)
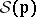 : $S ( D$
(confidence 0.16)
: $S ( D$
(confidence 0.16)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $> 7$
(confidence 0.68)
: $> 7$
(confidence 0.68)
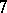 : $ $
(confidence 0.89)
: $ $
(confidence 0.89)
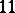 : $I$
(confidence 0.24)
: $I$
(confidence 0.24)
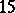 : $1.3$
(confidence 0.59)
: $1.3$
(confidence 0.59)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
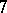 : $ $
(confidence 0.89)
: $ $
(confidence 0.89)
 : $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.56)
: $T ^ { 2 } \times Sp ( 1 )$
(confidence 0.56)
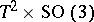 : $T ^ { 2 } \times SO ( 3 )$
(confidence 0.96)
: $T ^ { 2 } \times SO ( 3 )$
(confidence 0.96)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
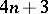 : $4 n + 3$
(confidence 1.00)
: $4 n + 3$
(confidence 1.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.89)
: $ $
(confidence 0.89)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
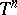 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
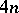 : $4 n$
(confidence 0.90)
: $4 n$
(confidence 0.90)
 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
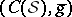 : $C ( s ) , g$
(confidence 0.71)
: $C ( s ) , g$
(confidence 0.71)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
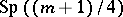 : $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.90)
: $\operatorname { sp } ( ( m + 1 ) / 4 )$
(confidence 0.90)
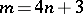 : $m = 4 n + 3$
(confidence 1.00)
: $m = 4 n + 3$
(confidence 1.00)
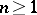 : $n > 1$
(confidence 0.99)
: $n > 1$
(confidence 0.99)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
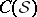 : $C ( S$
(confidence 0.88)
: $C ( S$
(confidence 0.88)
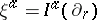 : $\xi ^ { d x } = I ^ { \alpha } ( \partial _ { \gamma } )$
(confidence 0.12)
: $\xi ^ { d x } = I ^ { \alpha } ( \partial _ { \gamma } )$
(confidence 0.12)
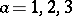 : $a = 1,2,3$
(confidence 0.89)
: $a = 1,2,3$
(confidence 0.89)
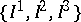 : $\{ I ^ { 1 } , R , \vec { P } \}$
(confidence 0.43)
: $\{ I ^ { 1 } , R , \vec { P } \}$
(confidence 0.43)
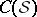 : $C ( S$
(confidence 0.88)
: $C ( S$
(confidence 0.88)
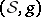 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
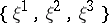 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
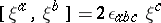 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
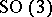 : $0 ( 3$
(confidence 0.45)
: $0 ( 3$
(confidence 0.45)
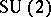 : $U ( 2 )$
(confidence 0.84)
: $U ( 2 )$
(confidence 0.84)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
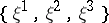 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
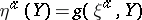 : $\eta ^ { \alpha } ( Y ) = g ( \xi ^ { d : } , Y )$
(confidence 0.15)
: $\eta ^ { \alpha } ( Y ) = g ( \xi ^ { d : } , Y )$
(confidence 0.15)
 : $\Phi ^ { d t } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.24)
: $\Phi ^ { d t } ( Y ) = \nabla _ { Y } \xi ^ { \alpha }$
(confidence 0.24)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
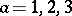 : $a = 1,2,3$
(confidence 0.89)
: $a = 1,2,3$
(confidence 0.89)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
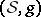 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
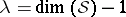 : $1 = \operatorname { dim } ( S ) - 1$
(confidence 0.40)
: $1 = \operatorname { dim } ( S ) - 1$
(confidence 0.40)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
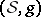 : $( S , g$
(confidence 0.32)
: $( S , g$
(confidence 0.32)
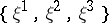 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
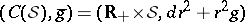 : $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.35)
: $( C ( S ) , \overline { g } ) = ( R _ { + } \times S , d r ^ { 2 } + r ^ { 2 } g )$
(confidence 0.35)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
: $\{ \xi ^ { 1 } , \xi ^ { 2 } , \xi ^ { 3 } \}$
(confidence 0.99)
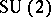 : $U ( 2 )$
(confidence 0.84)
: $U ( 2 )$
(confidence 0.84)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
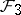 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
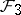 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
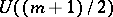 : $U ( ( m + 1 ) / 2 )$
(confidence 0.87)
: $U ( ( m + 1 ) / 2 )$
(confidence 0.87)
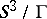 : $S ^ { 3 } / \Gamma$
(confidence 0.50)
: $S ^ { 3 } / \Gamma$
(confidence 0.50)
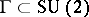 : $\subset \operatorname { SU } ( 2 )$
(confidence 0.30)
: $\subset \operatorname { SU } ( 2 )$
(confidence 0.30)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
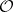 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
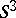 : $5 ^ { 2 }$
(confidence 0.10)
: $5 ^ { 2 }$
(confidence 0.10)
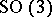 : $0 ( 3$
(confidence 0.45)
: $0 ( 3$
(confidence 0.45)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
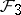 : $2 =$
(confidence 0.12)
: $2 =$
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
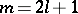 : $m = 2 l + 1$
(confidence 0.59)
: $m = 2 l + 1$
(confidence 0.59)
 : $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 0.99)
: $\tau = ( \tau _ { 1 } , \tau _ { 2 } , \tau _ { 3 } ) \in R ^ { 3 }$
(confidence 0.99)
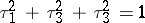 : $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.99)
: $\tau _ { 1 } ^ { 2 } + \tau _ { 3 } ^ { 2 } + \tau _ { 3 } ^ { 2 } = 1$
(confidence 0.99)
 : $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.81)
: $\xi ( \tau ) = \tau _ { 1 } \xi ^ { 1 } + \tau _ { 2 } \xi ^ { 2 } + \tau _ { 3 } \xi ^ { 3 }$
(confidence 0.81)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $5$
(confidence 0.49)
: $5$
(confidence 0.49)
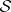 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
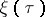 : $= T$
(confidence 0.36)
: $= T$
(confidence 0.36)
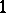 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
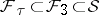 : $F _ { T } \subset F _ { 3 } \subset S$
(confidence 0.30)
: $F _ { T } \subset F _ { 3 } \subset S$
(confidence 0.30)
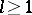 : $> 1$
(confidence 0.98)
: $> 1$
(confidence 0.98)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
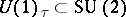 : $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.37)
: $U ( 1 ) _ { \tau } \subset SU ( 2 )$
(confidence 0.37)
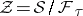 : $Z = S / F _ { T }$
(confidence 0.29)
: $Z = S / F _ { T }$
(confidence 0.29)
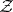 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
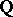 : $4$
(confidence 0.62)
: $4$
(confidence 0.62)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
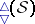 : $\Delta ( S )$
(confidence 0.50)
: $\Delta ( S )$
(confidence 0.50)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.12)
: $ $
(confidence 0.12)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
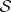 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
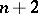 : $n + 2$
(confidence 1.00)
: $n + 2$
(confidence 1.00)
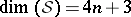 : $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.51)
: $\operatorname { dim } ( S ) = 4 n + 3$
(confidence 0.51)
 : $ $
(confidence 0.00)
: $ $
(confidence 0.00)
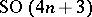 : $S O ( 4 n + 3 )$
(confidence 0.49)
: $S O ( 4 n + 3 )$
(confidence 0.49)
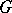 : $x$
(confidence 0.41)
: $x$
(confidence 0.41)
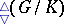 : $\hat { \gamma } ( G / K )$
(confidence 0.22)
: $\hat { \gamma } ( G / K )$
(confidence 0.22)
Maximilian Janisch/latexlist. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist&oldid=43669