Talk:Elementary matrix
From Encyclopedia of Mathematics
Revision as of 18:49, 20 March 2015 by Neo razgriz (talk | contribs) (Added another case where theorems based on the current definition are incorrect.)
Issue
This definition excludes the row-switching elementary matrix[1]:
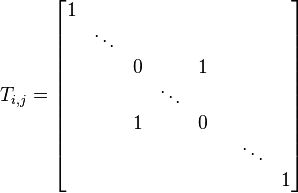
Proof
The matrix above (marked T) has more than one off-diagonal element added to it.
In addition, at least one diagonal element has been modified.
Therefore, by the definition on the Elementary matrix page, T is not an elementary matrix.
Alternate definition
In mathematics, an elementary matrix is a matrix which differs from the identity matrix by one single elementary row operation.[2]
References
--Ben Paradise (talk) 14:24, 20 March 2015 (CET)
- Thank you. Probably you are right. But, being not an algebraist, I am not sure: maybe different (non-equivalent) definitions are in use? Boris Tsirelson (talk) 19:13, 20 March 2015 (CET)
- Thanks for the reply. I also noticed that the same issue exists for Row-multiplying transformations.
- Theorems regarding the connection between row operations and elementary matrices are based on this definition.
- Pending review by an Algebraist. --Ben Paradise (talk) 19:49, 20 March 2015 (CET)
How to Cite This Entry:
Elementary matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_matrix&oldid=36335
Elementary matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_matrix&oldid=36335