Grothendieck group
of an additive category
An Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let $C$ be a small additive category with set of objects $\mathrm{Ob}(C)$ and let $G$ be an Abelian group. A mapping $\phi: \mathrm{Ob}(C) \to G$ is said to be additive if for any exact sequence $0 \to L \to M \to N \to 0$ in $C$, the relation $\phi(M)=\phi(L)+\phi(N)$ is valid. There exists a group $K(C)$, called the Grothendieck group of $C$, and an additive mapping $k:\mathrm{Ob}(C)\to K(C)$, known as the universal mapping, such that for any additive mapping $\mathrm{Ob}(C) \to G$, there exists a unique homomorphism $\xi: K(C) \to G$ that satisfies the condition $\phi=\xi \circ k$.
This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See 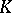 -functor in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$.
-functor in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$.
If $X$ is a topological space, then the Grothendieck group of the additive category of vector bundles over $X$ is an invariant of the space, studied in (topological) K-theory. If $C$ is the category of non-degenerate symmetric bilinear forms on linear spaces over a field $k$, then $K(C)$ is the Witt–Grothendieck group of $k$ (cf. Witt ring).
References
| [1] | R. Swan, "The Grothendieck ring of a finite group" Topology , 2 (1963) pp. 85–110 MR0153722 Zbl 0119.02905 |
| [2] | A. Borel, J.P. Serre, "Le théorème de Riemann–Roch" Bull. Soc. Math. France , 86 (1958) pp. 97–136 MR116022 Zbl 0091.33004 |
| [3] | M.F. Atiyah, "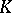 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [4] | H. Bass, "Lectures on topics in algebraic  -theory" , Tata Inst. (1966) -theory" , Tata Inst. (1966) |
| [5] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
Comments
One also associates a Grothendieck group $K(M)$ to any commutative monoid as the solution of the universal problem posed by additive mappings of $M$ into Abelian groups. It is the Abelian group with generators $m \in M$ and relations $m-m_1-m_2$, for all $m,m_1,m_2 \in M$ such that $m=m_1+m_2 in $M$. Taking, for instance, the monoid of isomorphism classes of vector bundles over a topological space $X$ (with the monoid addition induced by the direct sum) one again obtains the topological K-group $K(X)$. When considering an additive category $C$ in which not every short exact sequence splits, there are two possible natural associated Grothendieck groups. Both are Abelian groups generated by the isomorphism classes of objects of $C$. For the first there is a relation $[M]-[M_1]-[M_2]$ whenever $M$ is isomorphic to $M_1 \oplus M_2$, and for the second there is a relation $[M]-[M_1]-[M_2]$ whenever there is a short exact sequence $0 \to M_1 \to M \to M_2 \to 0$. Both notions occur in the literature. The Grothendieck group $K_0(A)$ defined by the additive category of finitely-generated projective modules over a ring $A$ (in which every short exact sequence splits of course) is sometimes called the Grothendieck group of the ring $A$. Cf. also [[Algebraic K-theory|Algebraic K-theory]]. Another important example of a Grothendieck group is the [[Picard group|Picard group]] $\mathrm{Pic}(A)$ of a ring (or of a scheme). It is the Grothendieck group associated to the commutative monoid of isomorphism classes of rank 1 projective modules over $A$ with the addition induced by the tensor product over $A$.
References
| [a1] | H. Bass, "Algebraic  -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [a2] | M. Karoubi, "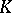 -theory" , Springer (1978) MR0488029 Zbl 0382.55002 -theory" , Springer (1978) MR0488029 Zbl 0382.55002 |
| [a3] | J. Berrick, "An approach to algebraic 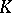 -theory" , Pitman (1982) MR649409 -theory" , Pitman (1982) MR649409 |
Grothendieck group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grothendieck_group&oldid=24624