Hölder space
A Banach space of bounded continuous functions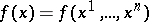 
defined on a set 
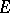of an 
-dimensional Euclidean space and satisfying a Hölder condition on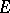 
.
The Hölder space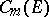 
, where 
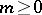is an integer, consists of the functions that are 
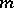times continuously differentiable on 
(continuous for 
).
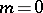The Hölder space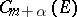 
, 
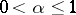, where 
is an integer, consists of the functions that are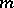 
times continuously differentiable (continuous for 
) and whose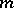 
-th derivatives satisfy the Hölder condition with index 
.
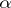For bounded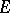 
a norm is introduced in 
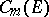and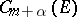 
as follows:
 |
 |
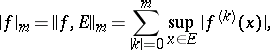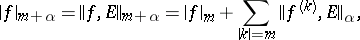where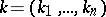 
, 
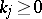is an integer,
 |
The fundamental properties of Hölder spaces for a bounded connected domain (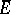
is the closure of 
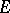) are:
1) 
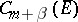is imbedded in 
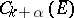if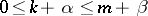 
, where 
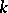and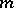 
are integers, 
, 
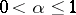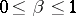. Here 
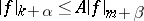and the constant 
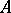is independent of 
.
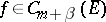2) The unit ball of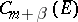 
is compact in 
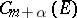if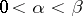 
. Consequently, any bounded set of functions from 
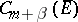contains a sequence of functions that converges in the metric of 
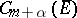to a function of 
.
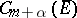References
| [1] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
Comments
If, in the above,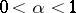 
, then 
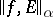is the Hölder 
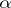-semi-norm of 
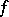on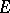 
, i.e.
 |
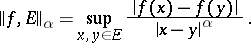See Hölder condition, where this norm is denoted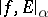 
.
Hölder spaces play a role in partial differential equations, potential theory, complex analysis, functional analysis (cf. Imbedding theorems), etc.
Hölder space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H%C3%B6lder_space&oldid=23330