Riemann-Hurwitz formula
Hurwitz formula, Hurwitz theorem
A formula that connects the genus and other invariants in a covering of Riemann surfaces (cf. Riemann surface). Let  and
and 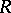 be closed Riemann surfaces, and let
be closed Riemann surfaces, and let 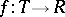 be a surjective holomorphic mapping. Suppose this is an
be a surjective holomorphic mapping. Suppose this is an 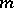 -sheeted covering, and suppose that
-sheeted covering, and suppose that 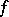 is branched in the points
is branched in the points 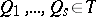 with multiplicities
with multiplicities 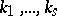 . Suppose that
. Suppose that  and
and  . Then the following (Riemann–Hurwitz) formula holds:
. Then the following (Riemann–Hurwitz) formula holds:
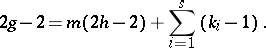 | (*) |
In particular, if  is the Riemann sphere, i.e.
is the Riemann sphere, i.e. 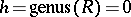 , then
, then
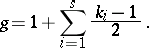 |
Formula (*) was stated by B. Riemann [1] and proved by A. Hurwitz [2].
In the case of coverings of complete curves over a field, an analogous formula can be derived in case the covering mapping  is separable (cf. Separable mapping). In that case
is separable (cf. Separable mapping). In that case
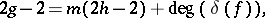 |
where 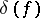 is the different of
is the different of 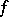 . In this case one speaks of the Riemann–Hurwitz–Hasse formula. In case a branching multiplicity
. In this case one speaks of the Riemann–Hurwitz–Hasse formula. In case a branching multiplicity 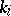 is divisible by the characteristic of the base field, one speaks of wild ramification, and the degree of
is divisible by the characteristic of the base field, one speaks of wild ramification, and the degree of 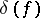 at that point is larger than
at that point is larger than  .
.
References
| [1] | B. Riemann, "Gesammelte mathematische Werke" , Dover, reprint (1953) |
| [2] | A. Hurwitz, "Ueber Riemann'sche Flächen mit gegebenen Verzweigungspunkte" , Mathematische Werke , 1 , Birkhäuser (1932) pp. 321–383 |
| [3] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) MR0173749 Zbl 0135.12101 |
| [4] | R. Nevanlinna, "Uniformisierung" , Springer (1967) MR0228671 Zbl 0152.27401 |
| [5] | S. Lang, "Introduction to algebraic and Abelian functions" , Addison-Wesley (1972) MR0327780 Zbl 0255.14001 |
Comments
The different of a mapping 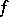 is the different of the extension of algebraic function fields determined by
is the different of the extension of algebraic function fields determined by  . For the latter notion cf. (the editorial comments to) Discriminant.
. For the latter notion cf. (the editorial comments to) Discriminant.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
| [a2] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 216–219 MR0507725 Zbl 0408.14001 |
| [a3] | H. Hasse, "Theorie der relativ-zyklischen algebraischen Funktionenkörper, insbesondere bei eindlichem Konstantenkörper" Reine Angew. Math. , 172 (1935) pp. 37–54 |
| [a4] | H.M. Farkas, I. Kra, "Riemann surfaces" , Springer (1980) pp. Sect. III.6 MR0583745 Zbl 0475.30001 |
Riemann-Hurwitz formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann-Hurwitz_formula&oldid=22981