Lévy-Khinchin canonical representation
A formula for the logarithm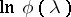 
of the characteristic function of an infinitely-divisible distribution:
 |
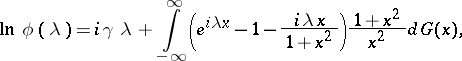where the integrand is equal to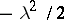 
for 
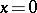and the characteristics 
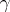and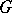 
are such that 
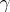is a real number and 
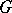is a non-decreasing left-continuous function of bounded variation.
The Lévy–Khinchin canonical representation was proposed by A.Ya. Khinchin (1937) and is equivalent to a formula proposed a little earlier by P. Lévy (1934) and called the Lévy canonical representation. To each infinitely-divisible distribution corresponds a unique set of characteristics 
and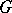 
in the Lévy–Khinchin canonical representation, and conversely, for any 
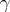and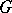 
as above, the Lévy–Khinchin canonical representation determines the logarithm of the characteristic function of an infinitely-divisible distribution. For the weak convergence of the sequence of infinitely-divisible distributions determined by characteristics 
, 
, 
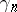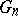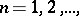to a distribution (which is necessarily infinitely divisible) with characteristics 
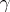and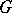 
it is necessary and sufficient that 
and that the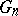 
converge weakly to 
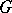as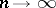 
.
For references see Lévy canonical representation.
Comments
For the notion of weak convergence see Distributions, convergence of.
Lévy-Khinchin canonical representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=L%C3%A9vy-Khinchin_canonical_representation&oldid=22733