De la Vallée-Poussin derivative
generalized symmetric derivative
A derivative defined by Ch.J. de la Vallée-Poussin [1]. Let 
be an even number and let there exist a 
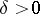such that for all 
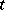with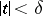 
,
 | (*) |
 |
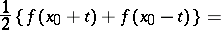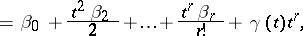where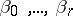 
are constants, 
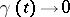as 
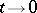and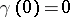 
. The number 
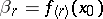is called the de la Vallée-Poussin derivative of order 
, or the symmetric derivative of order 
, of the function 
at the point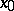 
.
The de la Vallée-Poussin derivatives of odd orders 
are defined in a similar manner, equation (*) being replaced by
 |
 |
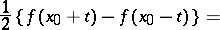The de la Vallée-Poussin derivative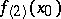 
is identical with Riemann's second derivative, often called the Schwarzian derivative. If 
exists, 
, 
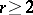, also exist, but 
need not exist. If there exists a finite ordinary two-sided derivative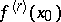 
, then 
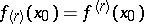. For the function 
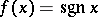, for example, 
, 
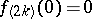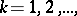and the 
, 
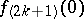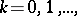do not exist. If there exists a de la Vallée-Poussin derivative 
, the series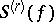 
obtained from the Fourier series of 
by term-by-term differentiation repeated 
times is summable at 
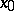to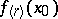 
by the method 
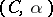for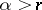 
, [2] (cf. Cesàro summation methods).
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur l'approximation des fonctions d'une variable reélle et de leurs dériveés par des polynômes et des suites limiteés de Fourier" Bull. Acad. Belg. , 3 (1908) pp. 193–254 |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) pp. Chapt.11 |
De la Vallée-Poussin derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_derivative&oldid=22325