Banach-Steinhaus theorem
A general appellation for several results concerning the linear-topological properties of the space of continuous linear mappings of one linear topological space into another. Let 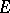 and
and 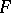 be locally convex linear topological spaces, where
be locally convex linear topological spaces, where 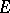 is a barrelled space, or let
is a barrelled space, or let 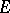 and
and 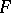 be linear topological spaces, where
be linear topological spaces, where 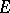 is a Baire space. The following propositions are then valid. 1) Any subset of the set
is a Baire space. The following propositions are then valid. 1) Any subset of the set 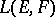 of continuous linear mappings of
of continuous linear mappings of 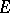 into
into 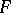 which is bounded in the topology of simple convergence is equicontinuous (the uniform boundedness principle); 2) If a filter
which is bounded in the topology of simple convergence is equicontinuous (the uniform boundedness principle); 2) If a filter 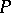 in
in 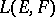 contains a set bounded in the topology of simple convergence, and converges in the topology of simple convergence to some mapping
contains a set bounded in the topology of simple convergence, and converges in the topology of simple convergence to some mapping  of
of 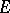 into
into 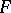 , then
, then  is a continuous linear mapping of
is a continuous linear mapping of 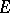 into
into 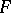 , and
, and 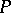 converges uniformly to
converges uniformly to  on each compact subset of
on each compact subset of 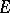 [2], [3].
[2], [3].
These general results make it possible to render the classical results of S. Banach and H. Steinhaus [1] more precise: Let 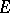 and
and 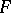 be Banach spaces and let
be Banach spaces and let 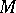 be a subset of the second category in
be a subset of the second category in 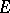 . Then, 1) if
. Then, 1) if 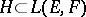 and
and 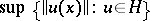 is finite for all
is finite for all 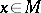 , then
, then 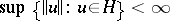 ; 2) if
; 2) if 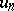 is a sequence of continuous linear mappings of
is a sequence of continuous linear mappings of 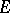 into
into 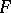 , and if the sequence
, and if the sequence 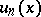 converges in
converges in 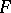 for all
for all 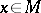 , then
, then 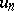 converges uniformly on any compact subset of
converges uniformly on any compact subset of 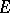 to a continuous linear mapping
to a continuous linear mapping  of
of 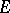 into
into 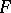 .
.
References
| [1] | S. Banach, H. Steinhaus, "Sur le principe de la condensation de singularités" Fund. Math. , 9 (1927) pp. 50–61 |
| [2] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) MR0583191 Zbl 1106.46003 Zbl 1115.46002 Zbl 0622.46001 Zbl 0482.46001 |
| [3] | H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) MR0193469 Zbl 0141.30503 |
Comments
References
| [a1] | G. Köthe, "Topological vector spaces" , 1 , Springer (1969) MR0248498 MR0178335 Zbl 0179.17001 |
| [a2] | J.L. Kelley, I. Namioka, "Linear topological spaces" , Springer (1963) MR0166578 Zbl 0115.09902 |
Banach-Steinhaus theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach-Steinhaus_theorem&oldid=22061