Carathéodory conditions
If one wants to relax the continuity assumption on a function 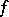 while preserving the natural equivalence between the Cauchy problem for the differential equation
while preserving the natural equivalence between the Cauchy problem for the differential equation 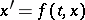 and the integral equation which can be obtained by integrating the Cauchy problem, one can follow ideas of C. Carathéodory [a1] and make the following definition.
and the integral equation which can be obtained by integrating the Cauchy problem, one can follow ideas of C. Carathéodory [a1] and make the following definition.
Let 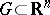 be an open set and
be an open set and  ,
, 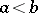 . One says that
. One says that 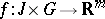 satisfies the Carathéodory conditions on
satisfies the Carathéodory conditions on 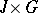 , written as
, written as 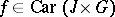 , if
, if
1) 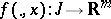 is measurable for every
is measurable for every 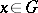 (cf. also Measurable function);
(cf. also Measurable function);
2) 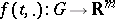 is continuous for almost every
is continuous for almost every 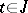 ;
;
3) for each compact set  the function
the function
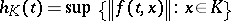 |
is Lebesgue integrable (cf. also Lebesgue integral) on 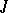 , where
, where  is the norm in
is the norm in 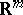 .
.
If 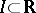 is a non-compact interval, one says that
is a non-compact interval, one says that 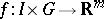 satisfies the local Carathéodory conditions on
satisfies the local Carathéodory conditions on 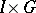 if
if 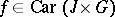 for every compact interval
for every compact interval 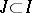 . This is written as
. This is written as 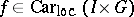 .
.
Note that any function 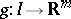 which is the composition of
which is the composition of 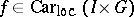 and a measurable function
and a measurable function  , i.e.
, i.e. 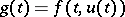 (cf. also Composite function), is measurable on
(cf. also Composite function), is measurable on 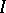 .
.
To specify the space of the majorant 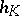 more precisely, one says that
more precisely, one says that 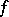 is
is 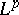 -Carathéodory,
-Carathéodory, 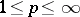 , if
, if 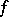 satisfies 1)–3) above with
satisfies 1)–3) above with 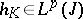 .
.
One can see that any function continuous on 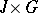 is
is 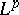 -Carathéodory for any
-Carathéodory for any 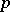 .
.
Similarly, one says that 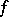 is locally
is locally 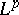 -Carathéodory on
-Carathéodory on 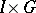 if
if 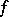 restricted to
restricted to 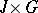 is
is 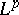 -Carathéodory for every compact interval
-Carathéodory for every compact interval 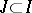 .
.
References
| [a1] | C. Carathéodory, "Vorlesungen über reelle Funktionen" , Dover, reprint (1948) |
| [a2] | E. Coddington, N. Levinson, "The theory of ordinary differential equations" , McGraw-Hill (1955) |
| [a3] | M.A. Krasnoselskij, "Topological methods in the theory of nonlinear integral equations" , Pergamon (1964) |
| [a4] | J. Kurzweil, "Ordinary differential equations" , Elsevier (1986) |
| [a5] | A.F. Filippov, "Differential equations with discontinuous right hand sides" , Kluwer Acad. Publ. (1988) |
Carathéodory conditions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory_conditions&oldid=19225