Discriminant
The discriminant of a polynomial 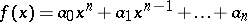 ,
, 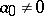 , whose roots are
, whose roots are  is the product
is the product
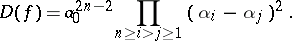 |
The discriminant vanishes if and only if the polynomial has multiple roots. The discriminant is symmetric with respect to the roots of the polynomial and may therefore be expressed in terms of the coefficients of this polynomial.
The discriminant of a quadratic polynomial 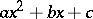 is
is 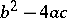 ; the discriminant of the polynomial
; the discriminant of the polynomial 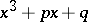 (the roots of which can be computed by the Cardano formula) is
(the roots of which can be computed by the Cardano formula) is 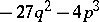 . If
. If 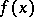 is a polynomial over a field of characteristic zero, then
is a polynomial over a field of characteristic zero, then
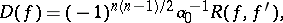 |
where 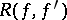 is the resultant of
is the resultant of 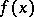 and its derivative
and its derivative 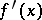 . The derivative of a polynomial
. The derivative of a polynomial 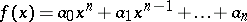 with coefficients from an arbitrary field is the polynomial
with coefficients from an arbitrary field is the polynomial 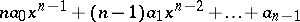 .
.
References
| [1] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) MR0945393 MR0926059 MR0778202 MR0759341 MR0628003 MR0384363 Zbl 0237.13001 |
Comments
References
| [a1] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [a2] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) MR0263582 Zbl 1032.00001 Zbl 1032.00002 |
The discriminant of a form 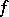 sesquilinear with respect to an automorphism
sesquilinear with respect to an automorphism 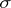 in a basis
in a basis 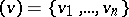 is the element of the ring
is the element of the ring 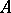 equal to
equal to
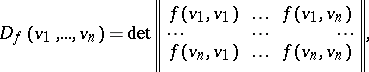 | (*) |
where 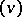 is a fixed basis of a free
is a fixed basis of a free 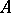 -module
-module 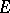 of finite rank over the commutative ring
of finite rank over the commutative ring 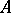 (with a unit element). If
(with a unit element). If 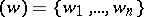 is another basis in
is another basis in 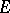 and if
and if
 |
is the transition matrix from  to
to 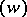 , then
, then
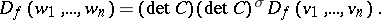 |
If 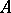 has no zero divisors, then for
has no zero divisors, then for 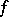 not to be degenerate it is necessary and sufficient that
not to be degenerate it is necessary and sufficient that
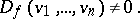 |
If  are
are  elements arbitrarily chosen from
elements arbitrarily chosen from 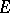 , then the element
, then the element 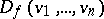 of
of 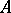 defined by (*) is called the discriminant of
defined by (*) is called the discriminant of 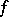 with respect to the system
with respect to the system  . Let
. Let 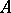 have no zero divisors and let
have no zero divisors and let 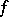 be a non-degenerate sesquilinear form. Then, for a system of elements
be a non-degenerate sesquilinear form. Then, for a system of elements  from
from 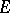 to be free it is necessary and sufficient that
to be free it is necessary and sufficient that 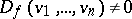 . Here,
. Here,  form a basis in
form a basis in 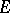 if and only if
if and only if 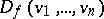 and
and  are associated in
are associated in 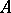 for some basis
for some basis  in
in 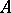 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) MR2333539 MR2327161 MR2325344 MR2284892 MR2272929 MR0928386 MR0896478 MR0782297 MR0782296 MR0722608 MR0682756 MR0643362 MR0647314 MR0610795 MR0583191 MR0354207 MR0360549 MR0237342 MR0205211 MR0205210 |
| [2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) Zbl 0221.20056 |
V.L. Popov
The discriminant of a system of elements of a field is one of the most important constructions in the theory of field extensions. Let 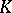 be a finite extension of a field
be a finite extension of a field 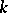 of degree
of degree  . The mapping from
. The mapping from 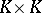 into
into 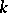 :
:
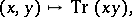 |
where 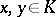 and
and 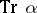 is the trace of an element
is the trace of an element 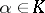 , is a symmetric bilinear form on the field
, is a symmetric bilinear form on the field 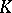 , which is regarded as a linear space over
, which is regarded as a linear space over 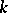 . The discriminant of this bilinear form (cf. Discriminant of a form) with respect to a system of elements
. The discriminant of this bilinear form (cf. Discriminant of a form) with respect to a system of elements 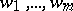 from
from 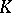 is said to be the discriminant of the system
is said to be the discriminant of the system 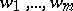 and is denoted by
and is denoted by 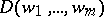 . In particular, if the system is a basis of
. In particular, if the system is a basis of 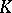 over
over 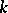 , its discriminant is called the discriminant of the basis of
, its discriminant is called the discriminant of the basis of 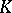 over
over 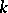 . The discriminants of two bases differ by a factor which is the square of some non-zero element of
. The discriminants of two bases differ by a factor which is the square of some non-zero element of 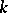 . The discriminant of any basis of
. The discriminant of any basis of 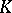 over
over  is non-zero if and only if the extension
is non-zero if and only if the extension 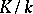 is separable (cf. Separable extension). If
is separable (cf. Separable extension). If 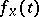 is a polynomial of degree
is a polynomial of degree 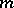 which is the minimal polynomial of the element
which is the minimal polynomial of the element  from the separable extension
from the separable extension 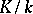 , then
, then 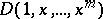 coincides with the discriminant of the polynomial
coincides with the discriminant of the polynomial 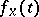 . The definitions above can also be applied to an arbitrary finite-dimensional associative algebra over a field (see 4) below).
. The definitions above can also be applied to an arbitrary finite-dimensional associative algebra over a field (see 4) below).
In the case of a separable extension 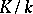 the discriminant of the basis
the discriminant of the basis  may be calculated by the formula
may be calculated by the formula
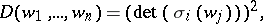 |
where  are all different imbeddings of
are all different imbeddings of  in a given algebraic closure of
in a given algebraic closure of 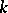 which leave
which leave 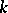 fixed.
fixed.
Let 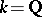 be the field of rational numbers, let
be the field of rational numbers, let 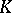 be an algebraic number field and let
be an algebraic number field and let 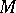 be some lattice of rank
be some lattice of rank  in
in 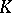 . Then, for any two bases of
. Then, for any two bases of 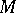 the values of discriminant are identical, and this common value is known as the discriminant of the lattice
the values of discriminant are identical, and this common value is known as the discriminant of the lattice 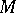 . If
. If 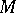 coincides with the ring of integers of the field
coincides with the ring of integers of the field 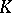 , the discriminant of
, the discriminant of  is simply called the discriminant of the field
is simply called the discriminant of the field 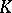 and is denoted by
and is denoted by 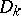 ; this quantity is an important characteristic of
; this quantity is an important characteristic of 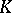 . For instance, if
. For instance, if 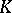 permits
permits  real and
real and 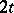 complex imbeddings in the field
complex imbeddings in the field 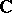 of complex numbers, then
of complex numbers, then
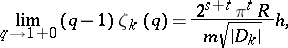 |
where 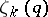 is Dedekind's zeta-function;
is Dedekind's zeta-function; 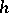 is the number of divisor classes,
is the number of divisor classes, 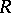 is the regulator of
is the regulator of 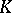 (cf. Regulator of an algebraic number field) and
(cf. Regulator of an algebraic number field) and 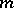 is the number of roots of unity in
is the number of roots of unity in 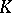 . By virtue of the estimate
. By virtue of the estimate
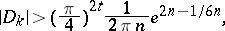 |
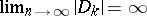 . For a quadratic field
. For a quadratic field 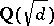 , where
, where 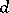 is a square-free rational integer,
is a square-free rational integer, 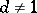 , one has the formulas
, one has the formulas
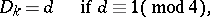 |
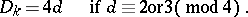 |
For a cyclotomic field 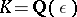 , where
, where  is a primitive
is a primitive 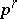 -th root of unity, one has
-th root of unity, one has
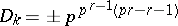 |
the minus sign being taken if 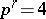 or
or 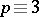 (
(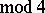 ), while the plus sign is taken in the other cases.
), while the plus sign is taken in the other cases.
This definition of the discriminant of a lattice in an algebraic number field may be generalized to the case when 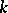 is the field of fractions of a Dedekind ring
is the field of fractions of a Dedekind ring 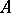 , and
, and 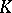 is a finite separable extension of
is a finite separable extension of 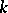 of degree
of degree  . Let
. Let 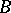 be the integral closure of the ring
be the integral closure of the ring 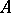 in
in 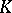 and let
and let 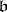 be an arbitrary fractional ideal in
be an arbitrary fractional ideal in 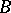 . Then the
. Then the 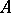 -module
-module 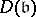 generated by all discriminants of the form
generated by all discriminants of the form 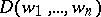 , where
, where  run through all possible bases of
run through all possible bases of 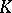 over
over 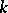 and lying in
and lying in 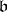 , is called the discriminant of the ideal
, is called the discriminant of the ideal 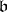 .
. 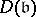 will then be a fractional ideal of
will then be a fractional ideal of 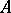 , and the equality
, and the equality 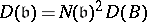 , where
, where 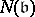 is the norm of the ideal
is the norm of the ideal 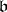 , is valid. The discriminant
, is valid. The discriminant 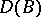 is identical with the norm of the different of the ring
is identical with the norm of the different of the ring 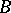 over
over 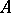 .
.
References
| [1] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) MR0195803 Zbl 0145.04902 |
| [2] | S. Lang, "Algebraic numbers" , Addison-Wesley (1964) MR0160763 Zbl 0211.38501 |
| [3] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) MR0389876 MR0384768 Zbl 0313.13001 |
| [4] | N. Jacobson, "The theory of rings" , Amer. Math. Soc. (1943) MR0008601 Zbl 0060.07302 |
V.L. Popov
The discriminant of an algebra 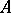 is the discriminant of the symmetric bilinear form
is the discriminant of the symmetric bilinear form 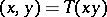 , where
, where 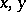 are elements of the finite-dimensional associative algebra
are elements of the finite-dimensional associative algebra 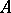 over a field
over a field 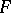 , while
, while 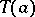 is the principal trace of the element
is the principal trace of the element 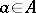 , which is defined as follows: Let
, which is defined as follows: Let  be some basis of the algebra
be some basis of the algebra 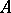 , let
, let 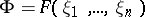 be a purely transcendental extension of the field
be a purely transcendental extension of the field 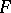 formed with algebraically independent elements
formed with algebraically independent elements 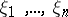 , and let
, and let 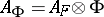 be the corresponding scalar extension of the algebra
be the corresponding scalar extension of the algebra 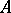 . An element
. An element 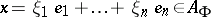 is then said to be a generic element of the algebra
is then said to be a generic element of the algebra 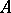 , while the minimal polynomial (over
, while the minimal polynomial (over 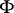 ) of the element
) of the element  is known as the minimal polynomial of the algebra
is known as the minimal polynomial of the algebra 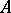 . Let
. Let
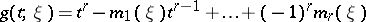 |
be the minimal polynomial of the algebra  ; the coefficients
; the coefficients 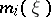 are in fact polynomials from
are in fact polynomials from 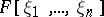 . If
. If 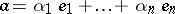 (
(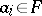 ) is an arbitrary element of
) is an arbitrary element of 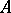 , then
, then 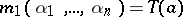 is said to be the principal trace of the element
is said to be the principal trace of the element  ,
, 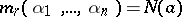 is said to be its principal norm, while the polynomial
is said to be its principal norm, while the polynomial 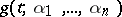 is known as its principal polynomial. For a given element
is known as its principal polynomial. For a given element 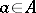 the coefficients of the principal polynomial are independent of the basis chosen; for this reason the bilinear form
the coefficients of the principal polynomial are independent of the basis chosen; for this reason the bilinear form 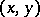 on
on  which was mentioned above is defined invariantly, while its discriminant is defined up to a multiplicative factor which is the square of a non-zero element of
which was mentioned above is defined invariantly, while its discriminant is defined up to a multiplicative factor which is the square of a non-zero element of 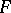 . The algebra
. The algebra 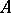 is separable (cf. Separable algebra) if and only if its discriminant is non-zero.
is separable (cf. Separable algebra) if and only if its discriminant is non-zero.
References
| [1] | N. Jacobson, "The theory of rings" , Amer. Math. Soc. (1943) MR0008601 Zbl 0060.07302 |
E.N. Kuz'min
Comments
Let 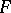 be a global field (an algebraic number field or a function field in one variable) or a local field, and let
be a global field (an algebraic number field or a function field in one variable) or a local field, and let 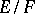 be a finite separable field extension. Let
be a finite separable field extension. Let 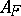 and
and 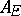 be the rings of integers (principal orders) of
be the rings of integers (principal orders) of 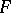 and
and 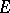 , respectively. Let
, respectively. Let 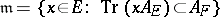 where
where 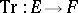 is the trace function.
is the trace function.
(Let 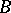 be a finite-dimensional commutative algebra over a field
be a finite-dimensional commutative algebra over a field 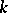 and
and 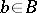 an element of
an element of 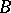 . Choose a basis
. Choose a basis  of
of 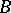 over
over 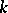 . Then multiplication with
. Then multiplication with 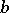 ,
, 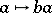 , is given by a certain matrix
, is given by a certain matrix 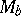 . One now defines, the trace, norm and characteristic polynomial of
. One now defines, the trace, norm and characteristic polynomial of 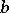 as the trace, determinant and characteristic polynomial of the matrix
as the trace, determinant and characteristic polynomial of the matrix 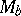 :
:
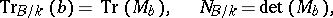 |
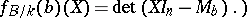 |
The set 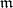 is a fractional ideal of
is a fractional ideal of 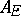 . Its inverse
. Its inverse  in the group of fractional ideals of the Dedekind ring
in the group of fractional ideals of the Dedekind ring 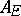 is called the different of the field extension
is called the different of the field extension 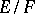 , and is denoted by
, and is denoted by 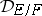 . Sometimes (if
. Sometimes (if 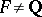 ) it is called the relative different, and the (absolute) different of
) it is called the relative different, and the (absolute) different of 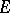 is then
is then 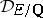 . If
. If 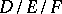 is a tower of field extensions one has the chain theorem for differents, also called multiplicativity of differents in a tower:
is a tower of field extensions one has the chain theorem for differents, also called multiplicativity of differents in a tower:
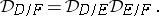 |
The ideal 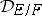 is an integral ideal of
is an integral ideal of 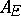 (i.e.
(i.e. 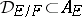 ) and it is related to the discriminant
) and it is related to the discriminant 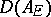 of the field extension
of the field extension 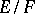 by
by
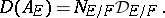 |
For the different 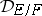 to be divisible by a prime ideal
to be divisible by a prime ideal 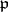 of
of 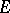 it is necessary and sufficient that
it is necessary and sufficient that 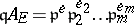 with
with  , where
, where 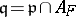 . This is Dedekind's discriminant theorem. Hence a prime ideal
. This is Dedekind's discriminant theorem. Hence a prime ideal 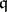 of
of 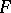 is ramified in
is ramified in 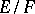 if and only if
if and only if 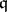 divides the discriminant
divides the discriminant 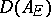 of
of 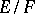 .
.
Given an additive subgroup 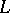 of
of 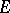 , its complementary set (relative to the trace) is defined by
, its complementary set (relative to the trace) is defined by
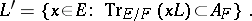 |
It is also an additive subgroup of 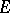 . Thus, the different of
. Thus, the different of 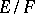 is the inverse of the complementary set of the ring of integers
is the inverse of the complementary set of the ring of integers 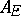 of
of 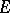 .
.
More generally one defines the different of an ideal  in
in 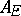 as the inverse of its complementary set:
as the inverse of its complementary set: 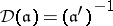 . It is again a (fractional) ideal of
. It is again a (fractional) ideal of 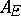 . The different of an element
. The different of an element  in
in 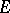 is defined as
is defined as 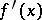 where
where 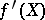 is the derivative of the characteristic polynomial
is the derivative of the characteristic polynomial 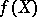 of the element
of the element  in
in 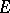 . If
. If 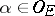 , then the different
, then the different 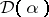 is in
is in 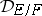 and
and 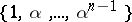 is an integral basis of
is an integral basis of 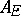 over
over 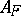 if and only if
if and only if 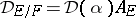 .
.
Let 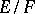 now be a finite extension of global fields. For each prime ideal
now be a finite extension of global fields. For each prime ideal 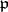 of
of 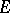 let
let 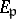 be the corresponding local field (the completion of
be the corresponding local field (the completion of 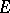 with respect to the
with respect to the 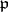 -adic topology on
-adic topology on 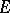 ). As before, if
). As before, if  is a prime ideal of
is a prime ideal of 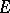 ,
, 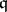 is the prime ideal of
is the prime ideal of 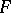 underneath it:
underneath it: 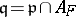 . Then one has for the local and global differents that
. Then one has for the local and global differents that
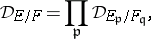 |
where an ideal 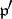 of
of 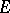 is identified with its completion in
is identified with its completion in 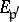 , and where the statement is supposed to include that all but finitely many of the factors on the right-hand side are 1, i.e. unit ideals (
, and where the statement is supposed to include that all but finitely many of the factors on the right-hand side are 1, i.e. unit ideals (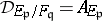 for almost-all
for almost-all 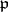 ).
).
Let now 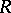 be a Dedekind integral domain with quotient field
be a Dedekind integral domain with quotient field 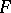 and let
and let 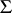 be a central simple algebra over
be a central simple algebra over 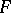 (i.e.
(i.e. 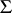 is a finite-dimensional associative algebra over
is a finite-dimensional associative algebra over 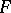 with no ideals except
with no ideals except  and
and 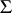 and the centre of
and the centre of 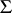 is
is 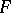 ). Then there is a separable normal extension
). Then there is a separable normal extension 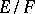 such that
such that 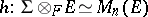 (as
(as 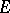 -algebras), where
-algebras), where 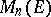 is the algebra of (
is the algebra of (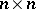 )-matrices over
)-matrices over 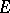 . (Such an
. (Such an 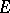 is called a splitting field for
is called a splitting field for 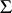 .) For each
.) For each 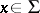 consider the element
consider the element 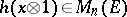 . The trace of this matrix is an element of
. The trace of this matrix is an element of 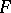 (not just of
(not just of 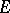 ); it is called the reduced trace and is denoted by
); it is called the reduced trace and is denoted by 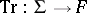 . (Its definition is also independent of the choice of
. (Its definition is also independent of the choice of 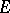 and
and 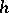 .) Similarly one defines the reduced norm,
.) Similarly one defines the reduced norm, 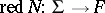 , as
, as 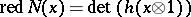 .
.
An 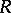 -lattice
-lattice  in
in 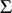 is an
is an 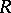 -submodule of
-submodule of 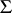 that is finitely generated over
that is finitely generated over 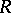 and is such that
and is such that  . An
. An 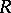 -lattice that is a subring and contains
-lattice that is a subring and contains 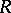 is called an order. A maximal order is an order that is not contained in any other. These always exist but may be non-unique. (These three definitions hold for any separable associative algebra over
is called an order. A maximal order is an order that is not contained in any other. These always exist but may be non-unique. (These three definitions hold for any separable associative algebra over 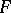 not just for central simple ones.)
not just for central simple ones.)
Let 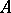 be a maximal order in
be a maximal order in  . The different of
. The different of  in this setting is defined by
in this setting is defined by  . The discriminant of a central simple algebra
. The discriminant of a central simple algebra 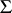 is the ideal
is the ideal 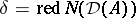 . It does not depend on the choice of the maximal order
. It does not depend on the choice of the maximal order  .
.
References
| [a1] | N. Jacobson, "Lectures in abstract algebra" , 3. Theory of fields and galois theory , v. Nostrand (1964) MR0172871 Zbl 0124.27002 |
| [a2] | S. Lang, "Algebraic numbers" , Addison-Wesley (1964) MR0160763 Zbl 0211.38501 |
| [a3] | A. Weil, "Basic number theory" , Springer (1967) MR0234930 Zbl 0176.33601 |
| [a4] | E. Weiss, "Algebraic number theory" , McGraw-Hill (1963) pp. Sects. 4–9 MR0159805 Zbl 0115.03601 |
Discriminant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discriminant&oldid=18875