Vinogradov-Goldbach theorem
From Encyclopedia of Mathematics
Revision as of 18:54, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Vinogradov–Goldbach theorem to Vinogradov-Goldbach theorem: ascii title)
A theorem on the representation of all sufficiently large odd numbers by a sum of three prime numbers. It is a consequence of the asymptotic formula for the number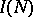 
of solutions of the equation
 |
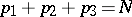in prime numbers, demonstrated by I.M. Vinogradov in 1937:
 |
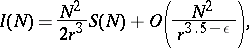where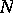 
is odd, 
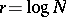and
 |
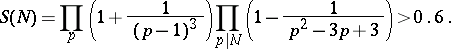Cf. Vinogradov method; Goldbach problem.
References
| [1] | I.M. Vinogradov, "Selected works" , Springer (1985) (Translated from Russian) |
| [2] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
How to Cite This Entry:
Vinogradov-Goldbach theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vinogradov-Goldbach_theorem&oldid=18790
Vinogradov-Goldbach theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vinogradov-Goldbach_theorem&oldid=18790
This article was adapted from an original article by A.A. Karatsuba (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article