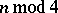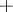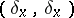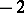Monodromy transformation

A transformation of the fibres (or of their homotopy invariants) of a fibre space corresponding to a path in the base. More precisely, let 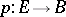be a locally trivial fibre space and let 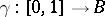be a path in 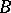with initial point 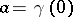and end-point 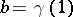. A trivialization of the fibration 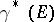defines a homeomorphism 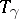of the fibre 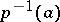onto the fibre 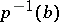, 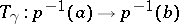. If the trivialization of 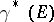is modified, then 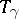changes into a homotopically-equivalent homeomorphism; this also happens if 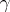is changed to a homotopic path. The homotopy type of 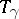is called the monodromy transformation corresponding to a path 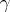. When 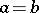, that is, when 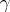is a loop, the monodromy transformation 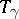is a homeomorphism of 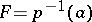into itself (defined, yet again, up to a homotopy). This mapping, and also the homomorphisms induced by it on the homology and cohomology spaces of 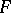, is also called a monodromy transformation. 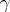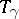The correspondence of with gives a representation of the fundamental group 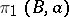on .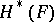

The idea of a monodromy transformation arose in the study of multi-valued functions (see Monodromy theorem). If 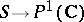is the Riemann surface of such a function, then by eliminating the singular points of the function from the Riemann sphere 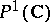, an unbranched covering is obtained. The monodromy transformation in this case is also called a covering or deck transformation.

The monodromy transformation arises most frequently in the following situation. Let 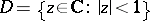be the unit disc in the complex plane, let 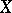be an analytic space, let 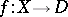be a proper holomorphic mapping (cf. Proper morphism), let 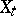be the fibre 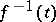, , 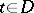, 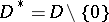and let 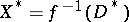. Diminishing, if necessary, the radius of 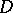, the fibre space 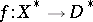can be made locally trivial. The monodromy transformation 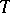associated with a circuit around in 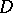is called the monodromy of the family 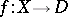at 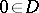, it acts on the (co)homology spaces of the fibre 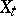, where . The most studied case is when 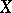and the fibres 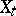, , 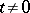are smooth. The action of 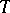on 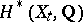, in this case, is quasi-unipotent [4], that is, there are positive integers 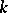and 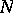such that 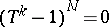. The properties of the monodromy display many characteristic features of the degeneracy of the family 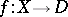. The monodromy of the family 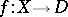is closely related to mixed Hodge structures (cf. Hodge structure) on the cohomology spaces 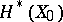and 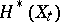(see [5]–[7]).

When the singularities of 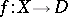are isolated, the monodromy transformation can be localized. Let be a singular point of 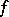(or, equivalently, of 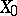) and let 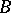be a sphere of sufficiently small radius in 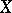with centre at . Diminishing, if necessary, the radius of 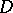, a local trivialization of the fibre space 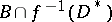can be defined. It is compatible with the trivialization of the fibre space 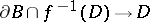on the boundary. This gives a diffeomorphism 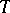of the manifold of "vanishing cycles" 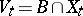into itself which is the identity on 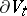, and which is called the local monodromy of 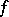at . The action of the monodromy transformation on the cohomology spaces 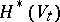reflects the singularity of 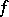at (see [1], [2], [7]). It is known that the manifold 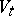is homotopically equivalent to a bouquet of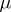 -dimensional spheres, where 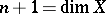and 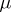is the Milnor number of the germ of 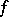at .

The simplest case is that of a Morse singularity when, in a neighbourhood of , 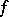reduces to the form 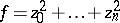(cf. Morse lemma). In this case 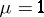, and the interior 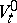of 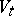is diffeomorphic to the tangent bundle of the -dimensional sphere 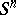. A vanishing cycle 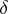is a generator of the cohomology group with compact support 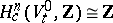, defined up to sign. In general, if 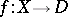is a proper holomorphic mapping (as above, having a unique Morse singularity at ), then a cycle 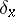vanishing at is the image of a cycle 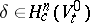under the natural mapping 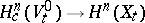. In this case the specialization homomorphism 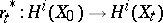is an isomorphism for 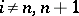, and the sequence

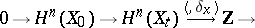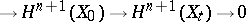is exact. The monodromy transformation 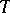acts trivially on 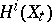for 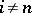and its action on is given by the Picard–Lefschetz formula: For ,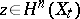

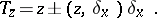The sign in this formula and the values of 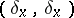are collected in the table.'

<tbody> </tbody>

A monodromy transformation preserves the intersection form on .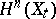

Vanishing cycles and monodromy transformations are used in the Picard–Lefschetz theory, associating the cohomology space of a projective complex manifold and its hyperplane sections. Let 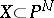be a smooth manifold of dimension 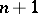, and let 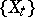, , 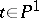be a pencil of hyperplane sections of 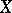with basic set (axis of the pencil) 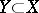; let the following conditions be satisfied: a) 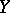is a smooth submanifold in 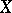; b) there is a finite set 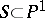such that 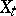is smooth for 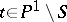; and c) for 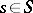the manifold 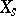has a unique non-degenerate quadratic singular point 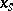, where 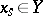. Pencils with these properties (Lefschetz pencils) always exist. Let 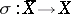be a monoidal transformation with centre on the axis 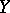of the pencil, and let 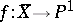be the morphism defined by the pencil 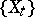; here 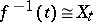for all 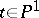. Let a point 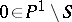be fixed; then the monodromy transformation gives an action of 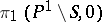on 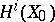(non-trivial only for 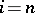). To describe the action of the monodromy on 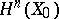one chooses points 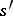, situated near 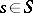, and paths 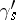leading from to . 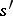Let 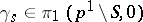be the loop constructed as follows: first go along 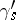, then once round and, finally, return along 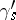to . 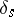In addition, let be a cycle vanishing at 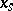(more precisely, take a vanishing cycle in 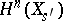and transfer it to 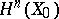by means of the monodromy transformation corresponding to the path 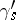). Finally, let 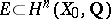be the subspace generated by the vanishing cycles 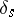, 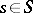(the vanishing cohomology space). Then the following hold.

1) 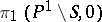is generated by the elements , ;

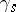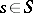2) the action of 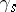is given by the formula

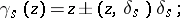3) the space 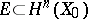is invariant under the action of the monodromy group ;

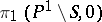4) the space of elements in 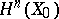that are invariant relative to monodromy coincides with the orthogonal complement of 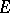relative to the intersection form on 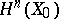, and also with the images of the natural homomorphisms 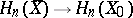and ;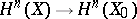

5) the vanishing cycles 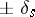are conjugate (up to sign) under the action of ;

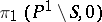6) the action of 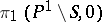on 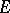is absolutely irreducible.

The formalism of vanishing cycles, monodromy transformations and the Picard–Lefschetz theory has also been constructed for 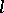-adic cohomology spaces of algebraic varieties over any field (see [3]).

References

[1]	V.I. Arnol'd, "Normal forms of functions in neighbourhoods of degenerate critical points" Russian Math. Surveys , 29 : 2 (1974) pp. 10–50 Uspekhi Mat. Nauk , 29 : 2 (1974) pp. 11–49 Zbl 0304.57018 Zbl 0298.57022
[2]	J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) MR0239612 Zbl 0184.48405
[3]	P. Deligne (ed.) N.M. Katz (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) MR0354657
[4]	C.H. Clemens, "Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities" Trans. Amer. Math. Soc. , 136 (1969) pp. 93–108 MR0233814 Zbl 0185.51302
[5]	W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 MR0382272 Zbl 0278.14003
[6]	J. Steenbrink, "Limits of Hodge structures" Invent. Math. , 31 (1976) pp. 229–257 MR0429885 Zbl 0303.14002
[7]	J.H.M. Steenbrink, "Mixed Hodge structure on the vanishing cohomology" P. Holm (ed.) , Real and Complex Singularities (Oslo, 1976). Proc. Nordic Summer School , Sijthoff & Noordhoff (1977) pp. 524–563 MR0485870 Zbl 0373.14007
[8]	S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1924) MR0033557 MR1520618
[9]	S. Lefschetz, "A page of mathematical autobiography" Bull. Amer. Math. Soc. , 74 : 5 (1968) pp. 854–879 MR0240803 Zbl 0187.18601