Semi-simple element
of a linear algebraic group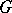 
An element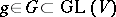 
, where 
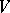is a finite-dimensional vector space over an algebraically closed field 
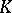, which is a semi-simple endomorphism of the space 
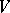, i.e. is diagonalizable. The notion of a semi-simple element of 
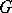is intrinsic, i.e. is determined by the algebraic group structure of 
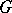only and does not depend on the choice of a faithful representation 
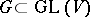as a closed algebraic subgroup of a general linear group. An element 
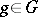is semi-simple if and only if the right translation operator 
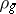in 
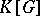is diagonalizable. For any rational linear representation 
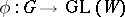, the set of semi-simple elements of the group 
is mapped onto the set of semi-simple elements of the group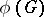 
.
Analogously one defines semi-simple elements of the algebraic Lie algebra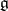 
of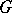 
; the differential 
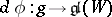of the representation 
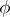maps the set of semi-simple elements of the algebra 
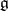onto the set of semi-simple elements of its image.
By definition, a semi-simple element of an abstract Lie algebra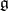 
is an element 
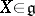for which the adjoint linear transformation 
is a semi-simple endomorphism of the vector space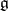 
. If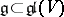 
is the Lie algebra of a reductive linear algebraic group, then 
is a semi-simple element of the algebra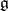 
if and only if 
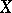is a semi-simple endomorphism of 
.
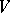References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
| [2] | Yu.I. Merzlyakov, "Rational groups" , Moscow (1980) (In Russian) MR0602700 Zbl 0518.20032 |
| [3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1975) MR0396773 Zbl 0325.20039 |
Comments
Thus, the notions of a semi-simple element for an algebraic Lie algebra (the Lie algebra of a linear algebraic group) and for an abstract Lie algebra do not necessarily coincide. But they do so for the Lie algebras of reductive linear algebraic groups (and semi-simple Lie algebras). To avoid this confusion, an element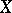 
of an abstract Lie algebra 
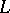such that ad 
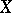is a semi-simple endomorphism of 
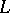is sometimes called 
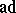-semi-simple.
Cf. also Jordan decomposition, 2).
References
| [a1] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 MR0323842 Zbl 0254.17004 |
| [a2] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) pp. LA6.14 (Translated from French) MR0218496 Zbl 0132.27803 |
Semi-simple element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-simple_element&oldid=18504