Lambda-calculus
lambda calculus.
Introduction.
The lambda calculus was introduced in 1932–1933 by A. Church
as part of a theory intended as a foundation for mathematics. This foundational theory consisted of a part dealing with logical symbols and rules and a part dealing with algorithms operating on these symbols. After it was shown by S.C. Kleene and J.B. Rosser [a7] that this foundational system was inconsistent, the part dealing with algorithms only was isolated as the (type-free) lambda calculus. It turned out to be quite successful in capturing the intuitive notion of computable function. Kleene [a6] showed that exactly the recursive functions (cf. Recursive function) are lambda definable in the sense given below. Then A.M. Turing [a10] introduced his machines (cf. Turing machine) and showed that Turing computable and lambda definable are equivalent notions. These are arguments for the Church–Turing thesis that the intuitive notion of computable is correctly formalised as lambda definable, Turing computable or recursive (cf. also Church thesis). Although many programming languages are based on the computational model of Turing (imperative programming), presently the model of Church enjoys a lot of attention in the form of functional programming.
Lambda terms.
Let  be an infinite set of variables. The set of lambda terms, notation
be an infinite set of variables. The set of lambda terms, notation  , is the least set satisfying: if
, is the least set satisfying: if  , then
, then  ; if
; if  , then
, then  ; if
; if  and
and  , then
, then 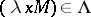 . The term
. The term 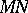 has as intended meaning:
has as intended meaning: 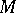 considered as function applied to
considered as function applied to  considered as argument;
considered as argument; 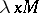 stands for the intuitive function that assigns to
stands for the intuitive function that assigns to  the value
the value  (possibly containing
(possibly containing  ). One uses
). One uses  for syntactic equality between terms. So
for syntactic equality between terms. So  and
and 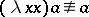 . Examples of
. Examples of  -terms are:
-terms are: 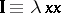 , the identity;
, the identity; 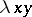 , the function with constant value
, the function with constant value 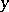 ; and
; and 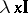 , the function with constant value
, the function with constant value  . Self-application is allowed:
. Self-application is allowed: 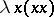 is a correct
is a correct 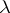 -term. In the expression
-term. In the expression  the occurrences of the variable
the occurrences of the variable  are said to be bound by
are said to be bound by 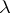 . If a variable occurrence is not bound, then it is said to be free in
. If a variable occurrence is not bound, then it is said to be free in 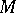 . A
. A 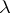 -term
-term  is closed if
is closed if 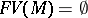 . E.g. in
. E.g. in 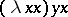 the variable
the variable  occurs free and bound and
occurs free and bound and 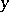 occurs free;
occurs free;  is a closed term. Terms that differ only in the names of bound variables are identified; e.g.
is a closed term. Terms that differ only in the names of bound variables are identified; e.g. 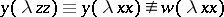 .
.
Conversion.
Following the intended meaning of the lambda expressions, the following so-called 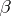 -rule is postulated as axiom:
-rule is postulated as axiom: 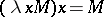 , or, more generally,
, or, more generally, 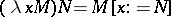 , where the right-hand side stands for the result of substituting
, where the right-hand side stands for the result of substituting 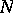 for the free occurrences of
for the free occurrences of  in
in 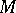 . When performing a substitution
. When performing a substitution 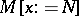 , care should be taken that no free variable in
, care should be taken that no free variable in 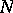 becomes bound. This can be accomplished by renaming all bound variables of
becomes bound. This can be accomplished by renaming all bound variables of  . E.g.
. E.g. 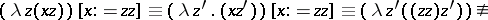
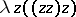 . If an equation
. If an equation  is provable from the
is provable from the 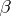 -rule alone, then one says that
-rule alone, then one says that 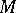 is convertible to
is convertible to 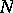 .
.
Currying.
Although abstraction is provided only to form unary functions, also functions of more arguments can be represented in lambda calculus by iterated abstraction. For example 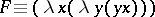 is a term such that
is a term such that 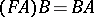 . (To make notation easier,
. (To make notation easier, 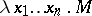 stands for
stands for 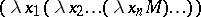 and
and 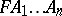 for
for 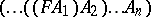 . Then one may write
. Then one may write 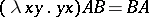 .) The method is due to M. Schönfinkel [a9] but is called currying after H.B. Curry who made it popular.
.) The method is due to M. Schönfinkel [a9] but is called currying after H.B. Curry who made it popular.
Representing computations.
From the 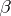 -rule one can prove the following fixed-point theorem. For all
-rule one can prove the following fixed-point theorem. For all 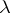 -terms
-terms 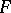 there exists a
there exists a 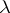 -term
-term 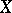 such that
such that 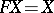 . (Indeed, a proof is as follows. Take
. (Indeed, a proof is as follows. Take 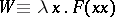 and
and 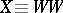 . Then
. Then 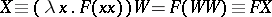 .) This result will be used to represent recursion. Write
.) This result will be used to represent recursion. Write 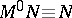 and
and 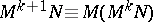 . Define for
. Define for 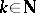 (the set of natural numbers) the
(the set of natural numbers) the 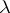 -term
-term 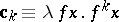 . The
. The 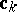 are called Church numerals. A function
are called Church numerals. A function 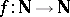 is said to be
is said to be 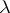 -definable if there exists a
-definable if there exists a 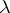 -term
-term  such that for all
such that for all  one has
one has 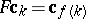 . This definition is extended to functions of more arguments by requiring e.g.
. This definition is extended to functions of more arguments by requiring e.g. 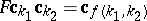 . Integer addition is
. Integer addition is 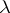 -definable using the term
-definable using the term  . The predecessor function is
. The predecessor function is  -defined by
-defined by 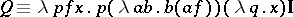 . Write
. Write  for
for 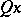 . Write
. Write 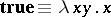 and
and 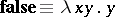 . Then "i fBthenXelseY" can be represented by
. Then "i fBthenXelseY" can be represented by 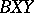 . Write
. Write 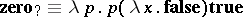 . Then
. Then 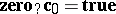 and
and 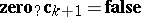 . Now suppose
. Now suppose 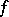 is defined by recursion, e.g.
is defined by recursion, e.g. 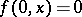 ,
, 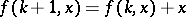 . Then it is possible to
. Then it is possible to  -define
-define 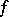 as follows. One wants an
as follows. One wants an 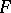 such that
such that 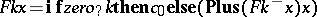 . This holds if
. This holds if 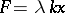 .
. 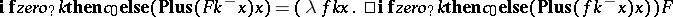 . Now
. Now 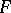 can be found using the fixed-point theorem. In a similar way minimalization (searching) can be represented by
can be found using the fixed-point theorem. In a similar way minimalization (searching) can be represented by 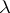 -terms.
-terms.
Reduction strategies.
If 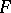
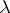 -defines a function
-defines a function  , then
, then 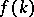 can be computed by evaluating
can be computed by evaluating 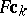 . Several strategies can be used in order to evaluate this
. Several strategies can be used in order to evaluate this 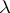 -term by giving priorities to the subexpressions
-term by giving priorities to the subexpressions 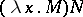 to be rewritten to
to be rewritten to 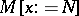 . (This replacement is called reduction.) If first the innermost such expressions are computed, then one has eager evaluation; if the outermost expressions are treated first, then one has lazy evaluation. For these and other reduction strategies, theoretical properties are given in [a1], Chapt. 13, and implementation issues are treated in [a4], Chapt. 9.
. (This replacement is called reduction.) If first the innermost such expressions are computed, then one has eager evaluation; if the outermost expressions are treated first, then one has lazy evaluation. For these and other reduction strategies, theoretical properties are given in [a1], Chapt. 13, and implementation issues are treated in [a4], Chapt. 9.
Types.
While 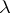 -terms can be used to represent algorithms, types serve to keep an order in these representing terms. (A similar role is played by dimensions of physical entities.) Let
-terms can be used to represent algorithms, types serve to keep an order in these representing terms. (A similar role is played by dimensions of physical entities.) Let 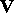 be a set of symbols considered as atomic types (
be a set of symbols considered as atomic types (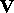 may e.g. contain nat and bool). Types form the least set
may e.g. contain nat and bool). Types form the least set 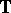 such that if
such that if 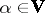 , then
, then 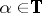 ; if
; if  , then
, then 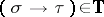 . A statement is of the form
. A statement is of the form 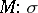 with
with 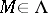 and
and 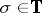 . The term
. The term 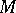 is the subject and
is the subject and 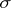 is the predicate of
is the predicate of  . A basis is a set of statements with only distinct variables as subjects. If
. A basis is a set of statements with only distinct variables as subjects. If 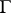 is a basis, then the notion
is a basis, then the notion 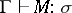 (read:
(read:  in
in 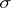 is derivable from
is derivable from 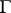 ; or:
; or: 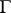 yields
yields 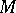 in
in  ) is the least relation satisfying: If
) is the least relation satisfying: If 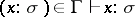 , if
, if 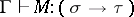 and
and  , then
, then 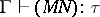 ; if
; if  ; then
; then 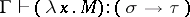 . Examples of valid derivable statements are the following:
. Examples of valid derivable statements are the following: 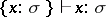 ,
, 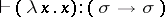 ,
, 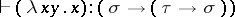 , and
, and 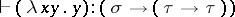 . The term
. The term  cannot be typed.
cannot be typed.
The following theorems hold: 1) If 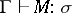 , then all reductions starting with
, then all reductions starting with 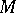 are terminating. 2) It is decidable whether, given a term
are terminating. 2) It is decidable whether, given a term 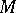 , there are
, there are 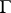 and
and  such that
such that 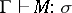 ; moreover, these
; moreover, these 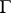 and
and  can be constructed if they exist. See e.g. [a5] for proofs.
can be constructed if they exist. See e.g. [a5] for proofs.
The programming language 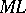 , see [a8], is based on the type-free lambda calculus in which to some terms types are assigned as above. The second theorem above makes it possible that the programmer does not need to write types: a compiler can construct them.
, see [a8], is based on the type-free lambda calculus in which to some terms types are assigned as above. The second theorem above makes it possible that the programmer does not need to write types: a compiler can construct them.
Semantics.
Since  -terms act at the same time as a function and as an argument, one would like to have a set
-terms act at the same time as a function and as an argument, one would like to have a set 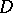 such that its function space
such that its function space 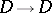 is in a one-to-one correspondence with
is in a one-to-one correspondence with 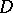 in order to give a semantics to
in order to give a semantics to 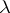 -terms. This is impossible for cardinality reasons. D.S. Scott constructed models for
-terms. This is impossible for cardinality reasons. D.S. Scott constructed models for 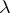 -terms by restricting
-terms by restricting  to the space of continuous functions from
to the space of continuous functions from 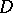 to
to  (for an appropriate notion of continuity) which has the same cardinality as
(for an appropriate notion of continuity) which has the same cardinality as 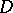 . A simple model in this style has been constructed by E. Engeler as follows. Let
. A simple model in this style has been constructed by E. Engeler as follows. Let 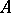 be a non-empty set. Let
be a non-empty set. Let  be the smallest set containing
be the smallest set containing 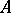 such that for
such that for  and finite
and finite 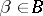 one has
one has 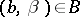 . Take
. Take 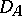 the collection of all subsets of
the collection of all subsets of 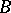 . A function
. A function 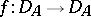 is called continuous if
is called continuous if 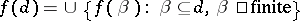 . For such
. For such  define
define 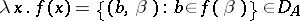 . In order to reconstruct
. In order to reconstruct 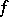 , form
, form 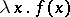 , define for
, define for 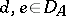 the application
the application 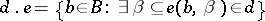 . Then
. Then 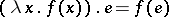 . Now
. Now 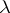 -terms can be interpreted in
-terms can be interpreted in 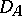 . Let a mapping
. Let a mapping 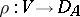 be given (environment). Define for
be given (environment). Define for 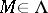 the element
the element 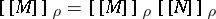 ,
, 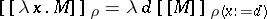 , where
, where 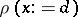 is the environment
is the environment 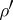 such that
such that 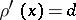 and
and 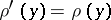 for
for 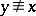 . In order that this definition makes sense it should be verified that
. In order that this definition makes sense it should be verified that 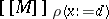 depends continuously on
depends continuously on  . This is the case because the application function is continuous in each of its variables.
. This is the case because the application function is continuous in each of its variables. 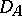 is a model of the
is a model of the  -calculus in the sense that if
-calculus in the sense that if  is provable, then
is provable, then  for each
for each 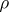 . It can be shown that terms with little computational effect, like
. It can be shown that terms with little computational effect, like 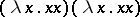 , have as image in
, have as image in 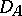 the empty set.
the empty set.
References
| [a1] | H.P. Barendregt, "The lambda-calculus, its syntax and semantics" , North-Holland (1984) |
| [a2] | H.P. Barendregt, "Lambda calculi with types" , Handbook of Logic in Computer Science , Oxford Univ. Press (To appear (1990)) |
| [a3a] | A. Church, "A set of postulates for the foundation of logic" Ann. of Math. (2) , 33 (1932) pp. 346–366 |
| [a3b] | A. Church, "A set of postulates for the foundation of logic" Ann. of Math. (2) , 34 (1933) pp. 839–864 |
| [a4] | A.J. Field, P.G. Harrison, "Functional programming" , Addison-Wesley (1988) |
| [a5] | J.R. Hindley, J.P. Seldin, "Introduction to combinators and lambda calculus" , Cambridge Univ. Press (1986) |
| [a6] | S.C. Kleene, "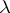 -definability and recursiveness" Duke Math. J. , 2 (1936) pp. 340–353 -definability and recursiveness" Duke Math. J. , 2 (1936) pp. 340–353 |
| [a7] | S.C. Kleene, J.B. Rosser, "The inconsistency of certain formal logics" Ann. of Math. (2) , 36 (1935) pp. 630–636 |
| [a8] | R. Milner, "A proposal for standard 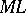 " , Proc. ACM Symp. on LISP and Functional Programming (Austin) (1984) pp. 184–197 " , Proc. ACM Symp. on LISP and Functional Programming (Austin) (1984) pp. 184–197 |
| [a9] | M. Schönfinkel, "Ueber die Bausteine der mathematische Logik" Math. Ann. , 92 (1924) pp. 305–316 |
| [a10] | A. Turing, "On computable numbers with an application to the Entscheidungsproblem" Proc. London Math. Soc. , 42 (1936) pp. 230–265 |
| [a11] | A. Turing, "Computability and 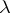 -definability" J. Symbolic Logic , 2 (1937) pp. 153–163 -definability" J. Symbolic Logic , 2 (1937) pp. 153–163 |
Lambda-calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambda-calculus&oldid=17754