Lie p-algebra
restricted Lie algebra
An algebra 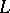 over a field
over a field 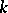 of characteristic
of characteristic 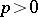 (or, more generally, over a ring of prime characteristic
(or, more generally, over a ring of prime characteristic 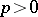 ), endowed with a
), endowed with a 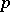 -mapping
-mapping 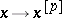 such that the following relations are satisfied:
such that the following relations are satisfied:
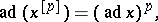 |
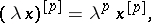 |
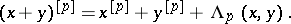 |
Here 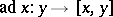 is the inner derivation of
is the inner derivation of  defined by the element
defined by the element  (the adjoint transformation) and
(the adjoint transformation) and 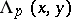 is a certain element of
is a certain element of 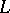 that is a linear combination of Lie monomials
that is a linear combination of Lie monomials
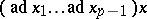 |
with 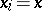 or
or 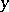 for all
for all 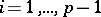 .
.
A typical example of a Lie 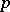 -algebra is obtained if one considers an arbitrary associative algebra
-algebra is obtained if one considers an arbitrary associative algebra 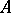 over
over 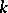 (cf. Associative rings and algebras) as a universal algebra, with the following two derivation operations:
(cf. Associative rings and algebras) as a universal algebra, with the following two derivation operations:
i) 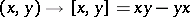 ,
,
ii) 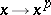 .
.
In particular, the property 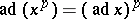 is a direct consequence of the identity
is a direct consequence of the identity
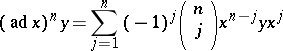 |
for 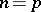 , in which case
, in which case 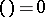 for
for  . Since any Lie algebra can be imbedded in a suitably chosen associative algebra
. Since any Lie algebra can be imbedded in a suitably chosen associative algebra 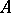 with the operations i) and ii) (the Poincaré–Birkhoff–Witt theorem), one often replaces
with the operations i) and ii) (the Poincaré–Birkhoff–Witt theorem), one often replaces 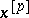 , with some risk of ambiguity, by
, with some risk of ambiguity, by 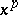 .
.
As in every structure theory, the structure-preserving mappings are of particular relevance.
For any Lie 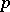 -algebra
-algebra 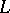 there is a
there is a 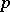 -universal (restricted universal) enveloping associative algebra
-universal (restricted universal) enveloping associative algebra 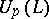 . If
. If 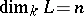 , then
, then 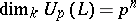 . This remark shows that for an arbitrary Lie algebra it makes sense to talk about its smallest
. This remark shows that for an arbitrary Lie algebra it makes sense to talk about its smallest 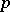 -envelope, or about its
-envelope, or about its 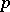 -closure.
-closure.
An ordinary Lie subalgebra 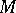 (Lie ideal) of
(Lie ideal) of 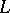 is called a
is called a 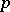 -subalgebra (
-subalgebra (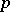 -ideal) if
-ideal) if 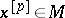 for all
for all 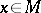 . A homomorphism
. A homomorphism 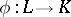 of Lie
of Lie 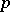 -algebras is called a
-algebras is called a 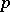 -homomorphism if
-homomorphism if
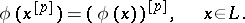 |
If 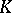 is a linear Lie
is a linear Lie 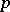 -algebra over
-algebra over  , one also calls this a
, one also calls this a 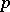 -representation
-representation 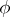 of
of 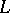 .
.
The specification of a 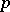 -structure
-structure  on a Lie algebra
on a Lie algebra 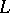 with basis
with basis  and zero centre
and zero centre 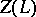 is uniquely and completely determined by specifying the images
is uniquely and completely determined by specifying the images 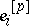 of the basis elements
of the basis elements 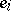 . On the other hand, a commutative Lie algebra
. On the other hand, a commutative Lie algebra 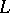 , for which one always has
, for which one always has 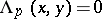 , is endowed with a
, is endowed with a 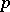 -structure by considering the pair
-structure by considering the pair 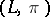 , where
, where 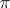 is an arbitrary
is an arbitrary 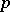 -semi-linear mapping,
-semi-linear mapping,
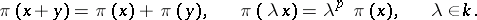 |
Over an algebraically closed field 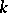 , every finite-dimensional commutative Lie
, every finite-dimensional commutative Lie 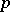 -algebra splits into the direct sum
-algebra splits into the direct sum 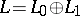 of a torus
of a torus
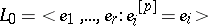 |
and a nilpotent subalgebra (cf. Nilpotent algebra) 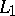 , where the identity
, where the identity
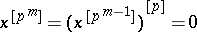 |
holds for sufficiently large 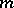 (see [1]).
(see [1]).
Important sources of Lie 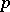 -algebras are the theory of algebraic groups, the theory of formal groups and the theory of inseparable fields (see [2]). The Lie algebra
-algebras are the theory of algebraic groups, the theory of formal groups and the theory of inseparable fields (see [2]). The Lie algebra 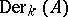 of all derivations of an arbitrary algebra
of all derivations of an arbitrary algebra  is a
is a 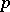 -subalgebra of
-subalgebra of 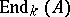 .
.
The class of simple Lie 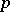 -algebras (restricted simple Lie algebras) is especially interesting for several reasons. For each finite-dimensional Lie algebra
-algebras (restricted simple Lie algebras) is especially interesting for several reasons. For each finite-dimensional Lie algebra 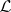 over the complex numbers
over the complex numbers 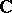 , let
, let 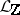 be the
be the 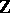 -span of a Chevalley basis of
-span of a Chevalley basis of 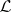 , and extend scalars to
, and extend scalars to 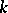 :
: 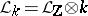 . The quotient algebra
. The quotient algebra 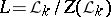 is simple and restricted. The simple Lie algebras obtained in this way are known as algebras of classical type:
is simple and restricted. The simple Lie algebras obtained in this way are known as algebras of classical type:  (
(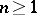 ),
), 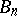 (
(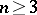 ),
), 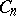 (
( ),
), 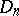 (
(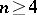 ),
), 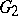 ,
, 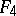 ,
, 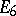 ,
, 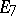 ,
, 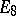 . Besides the classical algebras, there are four other classes of simple Lie
. Besides the classical algebras, there are four other classes of simple Lie 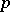 -algebras: general algebras
-algebras: general algebras 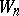 ,
, 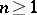 (
(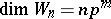 ); special algebras
); special algebras 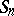 ,
, 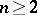 (
(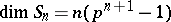 ); Hamiltonian algebras
); Hamiltonian algebras  ,
, 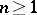 (
(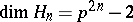 ); contact algebras
); contact algebras 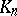 ,
, 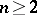 (
( , where
, where 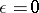 for
for 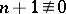 (
(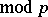 ) and
) and 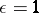 for
for 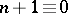 (
(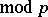 )). The simple Lie
)). The simple Lie 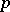 -algebras just described are called algebras of Cartan type. They are obtained by replacing the ring of power series
-algebras just described are called algebras of Cartan type. They are obtained by replacing the ring of power series 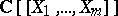 in the Lie–Cartan construction (see Lie algebra, 3)) by that of the
in the Lie–Cartan construction (see Lie algebra, 3)) by that of the 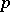 -truncated polynomials
-truncated polynomials 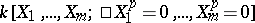 ,
, 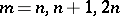 , or
, or 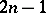 . In the symbols
. In the symbols 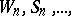 the index
the index  has an invariant meaning; namely, it is the dimension of a maximal toroidal subalgebra. The main Block–Wilson classification theorem [5]: Let
has an invariant meaning; namely, it is the dimension of a maximal toroidal subalgebra. The main Block–Wilson classification theorem [5]: Let 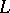 be a finite-dimensional simple Lie
be a finite-dimensional simple Lie 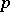 -algebra over an algebraically closed field
-algebra over an algebraically closed field 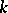 of characteristic
of characteristic 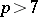 ; then
; then 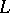 is of classical or Cartan type. This result was conjectured by A.I. Kostrikin and I.R. Shafarevich (see [3]). It is not known whether the statement above will be true for
is of classical or Cartan type. This result was conjectured by A.I. Kostrikin and I.R. Shafarevich (see [3]). It is not known whether the statement above will be true for 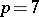 (presumably so), but for
(presumably so), but for 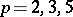 , however, the situation is necessarily more complicated. For example, for
, however, the situation is necessarily more complicated. For example, for 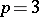 the classical Lie algebra
the classical Lie algebra 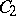 is included in a parametric family of
is included in a parametric family of 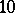 -dimensional simple Lie
-dimensional simple Lie 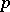 -algebras
-algebras 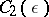 ,
, 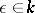 .
.
The theory of modular Lie algebras, i.e. Lie algebras over fields of characteristic 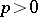 , was created in the last half-century. It is symbolically said that its source is the discovery of E. Witt (1937) of the simple non-classical Lie algebra
, was created in the last half-century. It is symbolically said that its source is the discovery of E. Witt (1937) of the simple non-classical Lie algebra 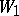 . Here it should be noted that there is a much more involved construction of the simple Lie algebras of Cartan type that are not
. Here it should be noted that there is a much more involved construction of the simple Lie algebras of Cartan type that are not 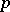 -algebras. By dropping the requirement of being restricted, additional difficulties arise also in the study of representations, cohomology, deformations, and other problems in the theory of modular Lie algebras. The study of interrelations between constructions taking these into account and not taking into account the restrictedness condition, forms an important part of the theory (cf. [6]).
-algebras. By dropping the requirement of being restricted, additional difficulties arise also in the study of representations, cohomology, deformations, and other problems in the theory of modular Lie algebras. The study of interrelations between constructions taking these into account and not taking into account the restrictedness condition, forms an important part of the theory (cf. [6]).
References
| [1] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201 |
| [2] | G.B. Seligman, "Modular Lie algebras" , Springer (1967) MR0245627 Zbl 0189.03201 |
| [3] | A.I. Kostrikin, I.R. Shafarevich, "Cartan pseudogroups and Lie 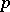 -algebras" Soviet Math. Dokl. , 7 (1986) pp. 715–718 Dokl. Akad. Nauk SSSR , 168 (1966) pp. 740–742 -algebras" Soviet Math. Dokl. , 7 (1986) pp. 715–718 Dokl. Akad. Nauk SSSR , 168 (1966) pp. 740–742 |
| [4] | H. Zassenhaus, "Ueber Liesche Ringe mit Primzahlcharacteristik" Abh. Math. Sem. Hansische Univ. , 13 (1939) pp. 1–100 |
| [5] | R.E. Block, R.L. Wilson, "Classification of the restricted simple Lie algebras" J. of Algebra , 114 (1988) pp. 115–259 MR0931904 |
| [6] | H. Strade, R. Farnsteiner, "Modular Lie algebras and their representations" , M. Dekker (1988) MR0929682 Zbl 0648.17003 |
Comments
In characteristic 2 and 3 there exist infinitely many simple Lie 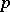 -algebras, of dimension 31 and 10, respectively (cf. [a1]).
-algebras, of dimension 31 and 10, respectively (cf. [a1]).
References
| [a1] | V.G. Kac, B.Yu. Veisfeiler, "Exponentials in Lie algebras of characteristic 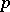 " Math. USSR Izv. , 5 (1971) pp. 777–803 Izv. Akad. Nauk SSSR , 35 (1971) pp. 762–788 MR0306282 Zbl 0252.17003 Zbl 0245.17007 " Math. USSR Izv. , 5 (1971) pp. 777–803 Izv. Akad. Nauk SSSR , 35 (1971) pp. 762–788 MR0306282 Zbl 0252.17003 Zbl 0245.17007 |
| [a2] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
Lie p-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_p-algebra&oldid=17551