Möbius series
A series of functions of the form
 | (*) |
These series were investigated by A. Möbius [1], who found for a series (*) the inversion formula
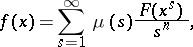 |
where 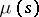 is the Möbius function. Möbius considered also inversion formulas for finite sums running over the divisors of a natural number
is the Möbius function. Möbius considered also inversion formulas for finite sums running over the divisors of a natural number  :
:
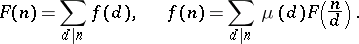 |
Another inversion formula: If 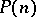 is a totally-multiplicative function (cf. Multiplicative arithmetic function) for which
is a totally-multiplicative function (cf. Multiplicative arithmetic function) for which 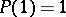 , and
, and 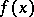 is a function defined for all real
is a function defined for all real 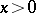 , then
, then
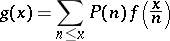 |
implies
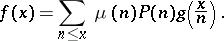 |
References
| [1] | A. Möbius, "Ueber eine besondere Art der Umkehrung der Reihen" J. Reine Angew. Math. , 9 (1832) pp. 105–123 |
| [2] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [3] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
Comments
All these (and many other) inversion formulas follow from the basic property of the Möbius function that it is the inverse of the unit arithmetic function 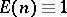 under the convolution product, cf. (the editorial comments to) Möbius function and Multiplicative arithmetic function.
under the convolution product, cf. (the editorial comments to) Möbius function and Multiplicative arithmetic function.
Möbius series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M%C3%B6bius_series&oldid=17395