Sheaf
A sheaf is a pre-sheaf 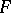 (cf. also Sheaf theory) on a topological space
(cf. also Sheaf theory) on a topological space 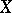 such that for every union
such that for every union 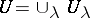 of open subsets
of open subsets 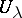 of
of 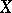 the following conditions are satisfied:
the following conditions are satisfied:
a) if on every 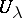 the restrictions of two elements
the restrictions of two elements  and
and 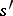 in
in 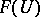 coincide, then
coincide, then  ;
;
b) if 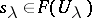 are such that for any pair of indices
are such that for any pair of indices  and
and 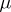 the restrictions of
the restrictions of 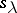 and
and 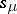 to
to 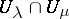 coincide, then there exists an element
coincide, then there exists an element 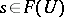 which on each
which on each 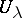 has restriction coinciding with
has restriction coinciding with 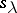 .
.
Every sheaf on  is isomorphic to the sheaf of continuous sections of a certain covering space
is isomorphic to the sheaf of continuous sections of a certain covering space 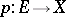 over
over 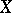 , which is determined uniquely up to an isomorphism (by a covering space one means a continuous mapping from
, which is determined uniquely up to an isomorphism (by a covering space one means a continuous mapping from  onto
onto  which is a local homeomorphism), therefore a sheaf is also commonly understood to be the covering space
which is a local homeomorphism), therefore a sheaf is also commonly understood to be the covering space 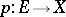 itself (see Sheaf theory).
itself (see Sheaf theory).
Comments
Generalizing the above notion of a sheaf on a topological space, it is also possible to define sheaves on an arbitrary site. Cf. also Topos.
For a more detailed treatment of sheaves, and additional references, see Sheaf theory.
References
| [a1] | G.E. Bredon, "Sheaf theory" , McGraw-Hill (1967) MR0221500 Zbl 0158.20505 |
| [a2] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) MR0102797 Zbl 0080.16201 |
Sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sheaf&oldid=17372