Carathéodory domain
A bounded simply-connected domain 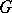 in the complex plane such that its boundary is the same as the boundary of the domain
in the complex plane such that its boundary is the same as the boundary of the domain 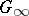 which is the component of the complement of
which is the component of the complement of 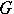 containing the point
containing the point 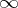 . A domain bounded by a Jordan curve is an example of a Carathéodory domain. Every Carathéodory domain is representable as the kernel of a decreasing convergent sequence of simply-connected domains
. A domain bounded by a Jordan curve is an example of a Carathéodory domain. Every Carathéodory domain is representable as the kernel of a decreasing convergent sequence of simply-connected domains 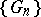 :
:
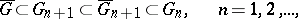 |
and every domain 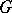 for which there exists such a sequence is a Carathéodory domain (Carathéodory's theorem, see [1]).
for which there exists such a sequence is a Carathéodory domain (Carathéodory's theorem, see [1]).
References
| [1] | C. Carathéodory, "Untersuchungen über die konformen Abbildungen von festen und veränderlichen Gebieten" Math. Ann. , 72 (1912) pp. 107–144 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Chapt. 2 (Translated from Russian) |
Comments
Let 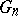 be a sequence of simply-connected domains in the complex plane. Suppose that each contains a fixed disc
be a sequence of simply-connected domains in the complex plane. Suppose that each contains a fixed disc 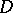 with centre
with centre 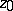 . Let
. Let 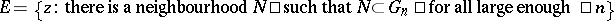 . Then
. Then 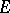 is open. Let
is open. Let 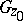 be the component of
be the component of 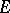 containing
containing 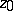 . This domain is called the kernel of the sequence
. This domain is called the kernel of the sequence 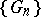 (relative to the point
(relative to the point 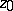 ). The sequence
). The sequence 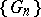 is said to converge to
is said to converge to 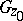 if every subsequence of
if every subsequence of 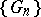 has the same kernel relative to
has the same kernel relative to 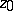 as
as 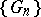 itself. Cf. [2].
itself. Cf. [2].
Carathéodory domain. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory_domain&oldid=17212