Hilbert-Schmidt norm
From Encyclopedia of Mathematics
Revision as of 18:52, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Hilbert–Schmidt norm to Hilbert-Schmidt norm: ascii title)
The norm of a linear operator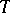 
acting from a Hilbert space 
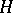into a Hilbert space 
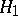, given by 
, where 
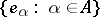is an orthonormal basis in 
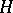. The Hilbert–Schmidt norm satisfies all the axioms of a norm and is independent of the choice of the basis. Its properties are: 
, 
, 
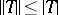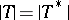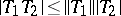, where 
is the norm of 
in the Hilbert space. If 
, then
 |
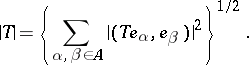References
| [1] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1968) (Translated from Russian) |
Comments
References
| [a1] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1981) (Translated from Russian) |
How to Cite This Entry:
Hilbert-Schmidt norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Schmidt_norm&oldid=16918
Hilbert-Schmidt norm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Schmidt_norm&oldid=16918
This article was adapted from an original article by V.B. Korotkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article