Predictable sigma-algebra
From Encyclopedia of Mathematics
predictable 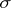 -algebra
-algebra
The least 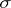 -algebra
-algebra 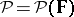 of sets in
of sets in
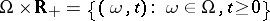 |
generated by all mappings 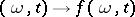 of the set
of the set 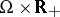 into
into 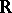 that are (for each fixed
that are (for each fixed 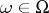 ) continuous from the left (in
) continuous from the left (in 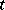 ) and
) and 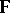 -adapted to a non-decreasing family
-adapted to a non-decreasing family 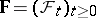 of sub-
of sub-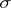 -algebras
-algebras 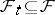 ,
, 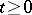 , where
, where 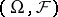 is a measurable space. A predictable
is a measurable space. A predictable 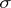 -algebra can be generated by any of the following families of sets:
-algebra can be generated by any of the following families of sets:
1) 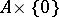 , where
, where 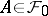 and
and 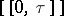 , where
, where  is a stopping time (cf. Markov moment) and
is a stopping time (cf. Markov moment) and 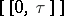 a stochastic interval;
a stochastic interval;
2) 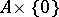 , where
, where 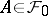 , and
, and 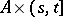 , where
, where 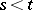 and
and  .
.
Between optional 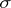 -algebras (cf. Optional sigma-algebra) and predictable
-algebras (cf. Optional sigma-algebra) and predictable 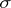 -algebras there is the relation
-algebras there is the relation  .
.
References
| [1] | C. Dellacherie, "Capacités et processus stochastique" , Springer (1972) |
Comments
Instead of "(s-) algebra" one more often uses (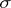 -) field.
-) field.
References
| [a1] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A-C , North-Holland (1978–1988) (Translated from French) |
How to Cite This Entry:
Predictable sigma-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predictable_sigma-algebra&oldid=16866
Predictable sigma-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Predictable_sigma-algebra&oldid=16866
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article