Multiplicity of a module
with respect to an ideal
Let 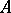 be a commutative ring with unit. A module
be a commutative ring with unit. A module 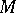 over
over 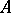 is said to be of finite length
is said to be of finite length  if there is a sequence of submodules (a Jordan–Hölder sequence)
if there is a sequence of submodules (a Jordan–Hölder sequence) 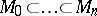 such that each of the quotients
such that each of the quotients 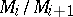 ,
, 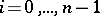 , is a simple
, is a simple 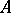 -module. (The number
-module. (The number  does not depend on the sequence chosen, by the Jordan–Hölder theorem.) Now let
does not depend on the sequence chosen, by the Jordan–Hölder theorem.) Now let  be an
be an 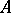 -module of finite type and
-module of finite type and  an ideal contained in the radical of
an ideal contained in the radical of 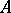 and such that
and such that 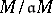 is of finite length, and let
is of finite length, and let  be of Krull dimension
be of Krull dimension 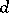 . (The Krull dimension of a module
. (The Krull dimension of a module  is equal to the dimension of the ring
is equal to the dimension of the ring 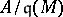 where
where 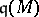 is the annihilator of
is the annihilator of 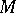 , i.e.
, i.e. 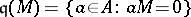 .) Then there exists a unique integer
.) Then there exists a unique integer 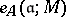 such that
such that
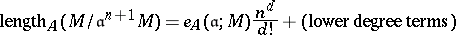 |
for  large enough. The number
large enough. The number  is called the multiplicity of
is called the multiplicity of 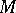 with respect to
with respect to  . The multiplicity of an ideal
. The multiplicity of an ideal  is
is 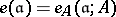 . Thus, the multiplicity of the maximal ideal
. Thus, the multiplicity of the maximal ideal 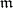 of a local ring
of a local ring  of dimension
of dimension 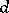 is equal to
is equal to 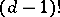 times the leading coefficient of the Hilbert–Samuel polynomial of
times the leading coefficient of the Hilbert–Samuel polynomial of 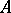 , cf. Local ring.
, cf. Local ring.
There are some mild terminological discrepancies in the literature with respect to the Hilbert–Samuel polynomial. Let 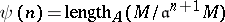 and
and 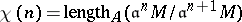 . Then both
. Then both 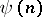 and
and 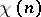 are sometimes called Hilbert–Samuel functions. For both
are sometimes called Hilbert–Samuel functions. For both 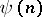 and
and 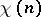 there are polynomials in
there are polynomials in  (of degree
(of degree 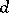 and
and 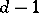 , respectively) such that
, respectively) such that 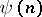 and
and 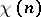 coincide with these polynomials for large
coincide with these polynomials for large  . Both these polynomials occur in the literature under the name Hilbert–Samuel polynomial.
. Both these polynomials occur in the literature under the name Hilbert–Samuel polynomial.
For a more general set-up cf. [a1].
The multiplicity of a local ring 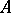 is the multiplicity of its maximal ideal
is the multiplicity of its maximal ideal 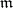 ,
, 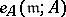 .
.
References
| [a1] | N. Bourbaki, "Algèbre commutative" , Masson (1983) pp. Chapt. 8, §4: Dimension MR2333539 MR2284892 MR0260715 MR0194450 MR0217051 MR0171800 Zbl 0579.13001 |
| [a2] | M. Nagata, "Local rings" , Interscience (1962) pp. Chapt. III, §23 MR0155856 Zbl 0123.03402 |
| [a3] | D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) pp. Appendix to Chapt. 6 MR0453732 Zbl 0356.14002 |
| [a4] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , v. Nostrand (1960) pp. Chapt. VIII, §10 MR0120249 Zbl 0121.27801 |
Multiplicity of a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplicity_of_a_module&oldid=16483