Poincaré theorem

Let a vector field 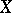be defined on a smooth closed two-dimensional Riemannian manifold 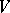(cf. Vector field on a manifold) and let it have a finite number of isolated singular points 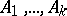. Then

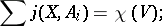here 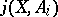is the index of the point 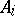with respect to 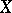(see Singular point, index of a) and 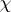is the Euler characteristic of 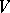. This was established by H. Poincaré (1881).

Comments

This theorem has since been established for manifolds of all dimensions, [a1].

An immediate consequence is that on a sphere 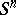of even dimension there is no continuous vector field without a zero (singularity), the Poincaré–Brouwer theorem, also called the hairy ball theorem. This was established for 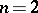by Poincaré and for 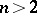by L.E.J. Brouwer. On the other hand, for the odd-dimensional spheres , , 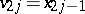, 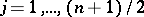gives a continuous vector field with no zeros on 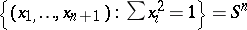. More generally one has that there exists a vector field without zero on a manifold 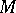if and only if 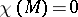, [a1].

References

[a1]	P.S. [P.S. Aleksandrov] Alexandroff, H. Hopf, "Topologie" , Chelsea, reprint (1972) pp. Chapt. XIV, Sect. 4.3
[a2]	M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 6