Fenchel-Moreau conjugate function
Given two sets  ,
,  and a "coupling" function
and a "coupling" function  , the Fenchel–Moreau conjugate to a function
, the Fenchel–Moreau conjugate to a function  with respect to the coupling function
with respect to the coupling function  is the function
is the function  defined by
defined by
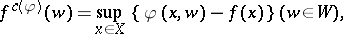 | (a1) |
with the convention  [a1]. When
[a1]. When  and
and 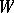 are linear spaces in duality, via a bilinear coupling function
are linear spaces in duality, via a bilinear coupling function 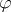 (cf. also Linear space; Duality),
(cf. also Linear space; Duality), 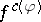 is just the usual Fenchel conjugate
is just the usual Fenchel conjugate 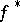 (called also the Young–Fenchel conjugate, or Legendre–Fenchel conjugate; cf. also Legendre transform) of
(called also the Young–Fenchel conjugate, or Legendre–Fenchel conjugate; cf. also Legendre transform) of 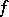 . If
. If 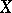 is a locally convex space and
is a locally convex space and 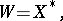 the conjugate space of
the conjugate space of 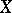 , with the coupling function
, with the coupling function 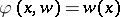 , then the second Fenchel conjugate
, then the second Fenchel conjugate 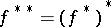 of
of 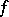 coincides with the greatest lower semi-continuous minorant of
coincides with the greatest lower semi-continuous minorant of 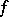 (Moreau's theorem); this result admits a natural extension to Fenchel–Moreau conjugates
(Moreau's theorem); this result admits a natural extension to Fenchel–Moreau conjugates 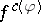 .
.
Another important particular class of Fenchel–Moreau conjugates is obtained for coupling functions 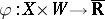 that take only the values
that take only the values  and
and  or, equivalently, the conjugates for which there exists a (unique) subset
or, equivalently, the conjugates for which there exists a (unique) subset  of
of 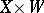 such that
such that
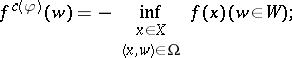 | (a2) |
these are called conjugates of type Lau or level-set conjugates. While Fenchel conjugates have many applications in convex analysis, conjugates of type Lau are useful for the study of quasi-convex functions (i.e., of functions all of whose level sets are convex) and for duality theory in micro-economics (duality between direct and indirect utility functions).
A useful related concept is the Flachs–Pollatschek conjugate function 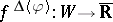 , defined by
, defined by
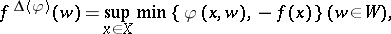 | (a3) |
which has applications in, e.g., optimization theory.
A unified approach is the conjugate function with respect to a binary operation  on
on  , assumed completely distributive (cf. also Completely distributive lattice) with respect to
, assumed completely distributive (cf. also Completely distributive lattice) with respect to 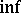 in the lattice
in the lattice 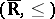 , defined by
, defined by
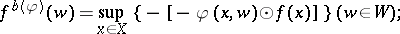 | (a4) |
in particular, when 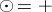 (respectively,
(respectively, 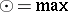 ),
), 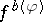 is the Fenchel–Moreau (respectively, the Flachs–Pollatschek) conjugate function of
is the Fenchel–Moreau (respectively, the Flachs–Pollatschek) conjugate function of  .
.
In another direction, the Fenchel–Moreau conjugate has been generalized to functions with values in extensions 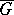 of ordered groups
of ordered groups 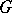 , with applications to functions in the extension (by adjoining
, with applications to functions in the extension (by adjoining 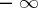 and
and 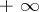 ) of the additive group
) of the additive group 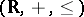 and to functions in the extension (by adjoining
and to functions in the extension (by adjoining  and
and 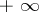 ) of the multiplicative group
) of the multiplicative group 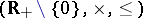 . More generally, one has also defined the conjugate function of
. More generally, one has also defined the conjugate function of 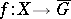 with respect to a binary operation
with respect to a binary operation  on
on 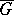 , encompassing the preceding conjugates as particular cases.
, encompassing the preceding conjugates as particular cases.
One of the main fields of applications of these concepts is optimization theory: When 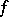 is the objective function of an optimization problem, a conjugate function is used to define (the objective function of) a "dual" optimization problem.
is the objective function of an optimization problem, a conjugate function is used to define (the objective function of) a "dual" optimization problem.
For more details, see [a2], [a3], [a4].
See also Conjugate function; Dual functions.
References
| [a1] | J.-J. Moreau, "Fonctions convexes en dualité" , Univ. Montpellier (1962) |
| [a2] | J. Flachs, M.A. Pollatschek, "Duality theorems for certain programs involving minimum or maximum operations" Math. Progr. , 16 (1979) pp. 348–370 |
| [a3] | W.E. Diewert, "Duality approaches to microeconomic theory" K.J. Arrow (ed.) M.D. Intrilligator (ed.) , Handbook of Mathematical Economics , 2 , North-Holland (1982) pp. 535–599 |
| [a4] | I. Singer, "Abstract convex analysis" , Wiley–Interscience (1997) |
Fenchel-Moreau conjugate function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fenchel-Moreau_conjugate_function&oldid=15994