Meusnier theorem
From Encyclopedia of Mathematics
If 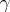 is a curve lying on a surface and
is a curve lying on a surface and 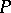 is a point on
is a point on 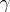 , then the curvature
, then the curvature 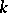 of
of 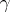 at
at 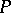 , the curvature
, the curvature 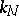 of the normal section of the surface by the osculating plane passing through the unit tangent to
of the normal section of the surface by the osculating plane passing through the unit tangent to 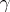 at
at 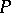 and the unit normal vector, and the angle
and the unit normal vector, and the angle 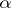 between the referred osculating plane of
between the referred osculating plane of 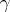 at
at 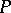 and any other osculating plane that does not go through the unit normal vector, satisfy the relation
and any other osculating plane that does not go through the unit normal vector, satisfy the relation
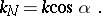 |
In particular, the curvature of every inclined section of the surface can be expressed in terms of the curvature of the normal section with the same tangent.
This theorem was proved by J. Meusnier in 1779 (and was published in [1]).
References
| [1] | J. Meusnier, Mém. prés. par div. Etrangers. Acad. Sci. Paris , 10 (1785) pp. 477–510 |
Comments
References
| [a1] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 142 |
| [a2] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
How to Cite This Entry:
Meusnier theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meusnier_theorem&oldid=15630
Meusnier theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Meusnier_theorem&oldid=15630
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article