Banach-Stone theorem
Stone–Banach theorem
For a compact Hausdorff space 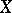 , let
, let 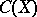 be the Banach space of all continuous scalar-valued functions on
be the Banach space of all continuous scalar-valued functions on 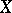 , with the usual
, with the usual 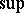 -norm:
-norm:
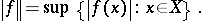 |
If 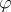 is a surjective homeomorphism from a compact space
is a surjective homeomorphism from a compact space 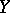 onto a compact space
onto a compact space 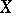 and
and 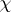 is a continuous and unimodular scalar-valued function on
is a continuous and unimodular scalar-valued function on 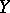 , then
, then
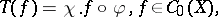 | (a1) |
defines a linear isometry from 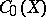 onto
onto  . The Banach–Stone theorem asserts that any linear surjective isometry
. The Banach–Stone theorem asserts that any linear surjective isometry 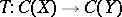 is of the above form. Here, if
is of the above form. Here, if  is not necessarily compact, then
is not necessarily compact, then 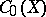 is the space of continuous functions that vanish at infinity (i.e. the functions
is the space of continuous functions that vanish at infinity (i.e. the functions  such that for all
such that for all  there is a compact set
there is a compact set 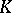 such that
such that  for
for  ). A unimodular function is one for which
). A unimodular function is one for which 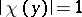 for all
for all 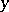 .
.
The theorem was proved in the real case for compact metric spaces by S. Banach [a2]; M.H. Stone [a10] proved that the assumption of metrizability was superfluous. Subsequently the theorem was extended to spaces of both real- or complex-valued functions defined on a locally compact Hausdorff space.
The theorem has been extended further into several directions:
1) a Banach space 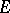 has the Banach–Stone property if the Banach space
has the Banach–Stone property if the Banach space 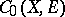 of
of 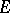 -valued continuous functions is isometric with
-valued continuous functions is isometric with 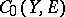 if and only if
if and only if  and
and  are homeomorphic; the class of Banach spaces with this property includes the strictly convex Banach spaces and the Banach spaces with strictly convex dual (see e.g. [a3], [a8]);
are homeomorphic; the class of Banach spaces with this property includes the strictly convex Banach spaces and the Banach spaces with strictly convex dual (see e.g. [a3], [a8]);
2) if there is an isomorphism 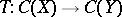 such that
such that 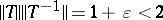 , then
, then 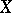 and
and 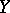 are homeomorphic (and consequently
are homeomorphic (and consequently 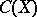 and
and 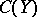 are isometric) [a1], [a4], where
are isometric) [a1], [a4], where  is the best bound [a5];
is the best bound [a5];
3) the theorem holds for several classes of subspaces of the spaces 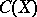 , the most important one being the class of uniform algebras (cf. also Uniform algebra).
, the most important one being the class of uniform algebras (cf. also Uniform algebra).
A joint approach to the last two extensions gave rise to the perturbation theory of uniform algebras. A Banach algebra 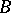 is an
is an  -perturbation (or
-perturbation (or  -metric perturbation) of a Banach algebra
-metric perturbation) of a Banach algebra 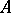 if there is an isomorphism
if there is an isomorphism  such that
such that 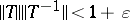 . In such a situation the algebras
. In such a situation the algebras 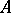 ,
,  must share several important properties [a7], [a9]; if the algebra
must share several important properties [a7], [a9]; if the algebra 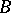 is forced to be isometrically isomorphic with
is forced to be isometrically isomorphic with 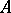 , the algebra
, the algebra  is called stable. Examples of stable uniform algebras include
is called stable. Examples of stable uniform algebras include 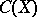 ,
, 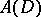 and
and 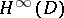 , with
, with  the unit disc.
the unit disc.
Isometries of several other classes of Banach spaces have been shown to follow the same general pattern, similar to (a1); one often refers to such results also as Banach–Stone theorems (for a given class of spaces; see e.g. [a6]).
References
| [a1] | D. Amir, "On isomorphisms of continuous function spaces" Israel J. Math. , 3 (1965) pp. 205–210 |
| [a2] | S. Banach, "Théorie des opérations linéaires" , PWN (1932) |
| [a3] | E. Behrends, "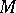 -structure and the Banach–Stone theorem" , Lecture Notes in Mathematics , 736 , Springer (1979) -structure and the Banach–Stone theorem" , Lecture Notes in Mathematics , 736 , Springer (1979) |
| [a4] | M. Cambern, "On isomorphisms with small bound" Proc. Amer. Math. Soc. , 18 (1967) pp. 1062–1066 |
| [a5] | H.B. Cohen, "A bound-two isomorphism between 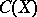 Banach spaces" Proc. Amer. Math. Soc. , 50 (1975) pp. 215–217 Banach spaces" Proc. Amer. Math. Soc. , 50 (1975) pp. 215–217 |
| [a6] | R.J. Fleming, J.E. Jamison, "Isometries on Banach spaces: a survey" , Analysis, Geometry and Groups: a Riemann Legacy Volume , Hadronic Press (1993) pp. 52–123 |
| [a7] | K. Jarosz, "Perturbations of Banach algebras" , Lecture Notes in Mathematics , 1120 , Springer (1985) |
| [a8] | K. Jarosz, "Small isomorphisms of 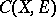 spaces" Pacific J. Math. , 138 : 2 (1989) pp. 295–315 spaces" Pacific J. Math. , 138 : 2 (1989) pp. 295–315 |
| [a9] | R. Rochberg, "Deformation of uniform algebras on Riemann surfaces" Pacific J. Math. , 121 : 1 (1986) pp. 135–181 |
| [a10] | M.H. Stone, "Applications of the theory of Boolean rings to general topology" Trans. Amer. Math. Soc. , 41 (1937) pp. 375–481 |
Banach-Stone theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach-Stone_theorem&oldid=15162