Laplace-Stieltjes transform
From Encyclopedia of Mathematics
Revision as of 18:53, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Laplace–Stieltjes transform to Laplace-Stieltjes transform: ascii title)
Let 
be a function of bounded variation on 
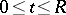, for all positive 
. The integral
 |
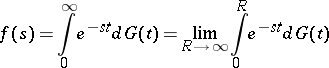is known as a (formal) Laplace–Stieltjes integral.
If the integral converges for some complex number 
, then it converges for all 
with 
, and the function 
is then the Laplace–Stieltjes transform of 
. If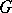 
is of the form 
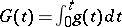for a functi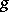on 
on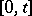 
that is Lebesgue integrable for all 
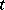(see Lebesgue integral), then the Laplace–Stieltjes transform becomes the Laplace transform 
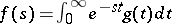of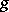 
.
There is also a corresponding two-sided Laplace–Stieltjes transform (or bilateral Laplace–Stieltjes transform) for suitable functions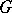 
.
See Laplace transform for additional references.
References
| [a1] | D.V. Widder, "An introduction to transform theory" , Acad. Press (1971) |
How to Cite This Entry:
Laplace-Stieltjes transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace-Stieltjes_transform&oldid=15100
Laplace-Stieltjes transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Laplace-Stieltjes_transform&oldid=15100
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article