Constructible subset
of an algebraic variety
A finite union of locally closed (in the Zariski topology) subsets. A locally closed subset is, by definition, an intersection of an open and a closed subset. The constructible subsets form a Boolean algebra and can be defined as elements of the Boolean algebra generated by the algebraic subvarieties. The role of constructible subsets in algebraic geometry is revealed by Chevalley's theorem: If 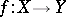 is a morphism of algebraic varieties, then
is a morphism of algebraic varieties, then 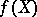 (and, moreover, the image of any constructible subset in
(and, moreover, the image of any constructible subset in 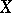 ) is a constructible subset in
) is a constructible subset in 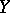 . This is related to the fact that "algebraic" conditions determine the constructible subsets of an algebraic variety.
. This is related to the fact that "algebraic" conditions determine the constructible subsets of an algebraic variety.
A mapping 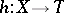 is called constructible if
is called constructible if 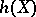 is finite and if for any point
is finite and if for any point 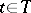 the pre-image
the pre-image 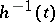 is a constructible subset in
is a constructible subset in 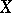 .
.
References
| [1] | A. Grothendieck, J. Dieudonné, "Eléments de géometrie algébrique" , I. Le langage des schémes , Springer (1971) MR0238860 MR0217086 MR0199181 MR0173675 MR0163911 MR0217085 MR0217084 MR0163910 MR0163909 MR0217083 MR0163908 Zbl 0203.23301 |
| [2] | A. Borel, "Linear algebraic groups" , Benjamin (1969) MR0251042 Zbl 0206.49801 Zbl 0186.33201 |
Constructible subset. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Constructible_subset&oldid=15045