De la Vallée-Poussin theorem
The de la Vallée-Poussin theorem on the distribution of prime numbers: Let 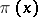 be the number of primes smaller than
be the number of primes smaller than  ; then, if
; then, if 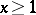 , the following equality is valid:
, the following equality is valid:
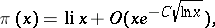 |
where 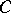 is a positive constant and
is a positive constant and 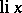 is the integral logarithm of
is the integral logarithm of  . This theorem demonstrates the correctness of Gauss' hypothesis on the distribution of prime numbers, viz., as
. This theorem demonstrates the correctness of Gauss' hypothesis on the distribution of prime numbers, viz., as 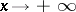 ,
,
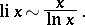 |
Established by Ch.J. de la Vallée-Poussin [1]. Cf. Distribution of prime numbers.
References
| [1] | Ch.J. de la Vallée-Poussin, "Recherches analytiques sur la théorie des nombers premiers" Ann. Soc. Sci. Bruxelles , 20 (1899) pp. 183–256 |
| [2] | Ch.J. de la Vallée-Poussin, "Sur la fonction 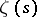 de Riemann et la nombre des nombres premiers inférieurs à une limite donnée" Mem. Couronnes Acad. Sci. Belg. , 59 : 1 (1899–1900) de Riemann et la nombre des nombres premiers inférieurs à une limite donnée" Mem. Couronnes Acad. Sci. Belg. , 59 : 1 (1899–1900) |
| [3] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
S.M. Vorazhin
The de la Vallée-Poussin alternation theorem: If a sequence of points 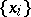 ,
, 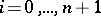 , in a closed set
, in a closed set 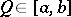 forms an alternation, then for the best approximation of a function
forms an alternation, then for the best approximation of a function 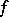 by polynomials of the form
by polynomials of the form
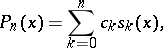 |
the estimate
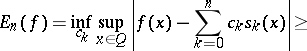 |
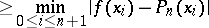 |
is valid, where 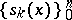 is a Chebyshev system. Established by Ch.J. de la Vallée-Poussin [1].
is a Chebyshev system. Established by Ch.J. de la Vallée-Poussin [1].
According to the Chebyshev theorem, equality holds if and only if 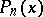 is the polynomial of best approximation. Analogues of this theorem exist for arbitrary Banach spaces [2]. The theorem is employed in numerical methods for constructing polynomials of best approximation.
is the polynomial of best approximation. Analogues of this theorem exist for arbitrary Banach spaces [2]. The theorem is employed in numerical methods for constructing polynomials of best approximation.
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur les polynômes d'approximation et la répresentation approchée d'un angle" Bull. Acad. Belg. , 12 (1910) pp. 808–845 |
| [2] | A.L. Garkavi, "The theory of approximation in normed linear spaces" Itogi Nauk. Mat. Anal. 1967 (1969) pp. 75–132 (In Russian) |
Yu.N. Subbotin
Comments
An account of the life and work of de la Vallée-Poussin can be found in, e.g., [a1].
A sequence of points 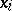 ,
, 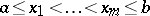 , is called an alternation for a continuous function
, is called an alternation for a continuous function 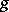 on
on 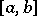 if
if 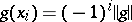 where
where 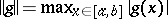 .
.
References
| [a1] | J. Favard, "Hommage à Charles de la Vallée Poussin (1866–1962)" P.L. Butzer (ed.) J. Korevaar (ed.) , On approximation theory , Birkhäuser (1964) pp. 1–3 |
| [a2] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) pp. 203ff |
De la Vallée-Poussin theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_theorem&oldid=14929